差分及树上差分的正确食用姿势（2019/2/21学习笔记）

1.啥是佩奇差分？

函数的前向差分通常简称为函数的差分。对于函数，在等距节点：

在oi界，差分一般指前向差分，即

f[x]=f[x]+f[x-1];

比如要在3~5这个区间内的值都加上2。

1.先在3的位置加上2。

由公式得

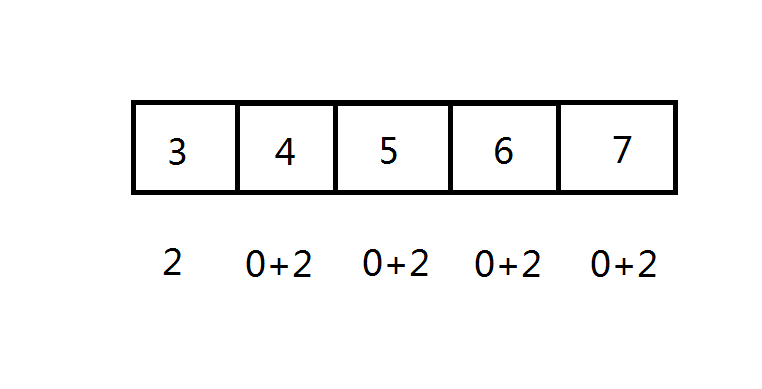
诶等等，不是说只是3~5区间内吗，怎么加到6，7去了？

得想个办法。

既然之前是加上了2，那就直接在超出去的位置再减掉就可以啦。

这不就对了。

所以差分的惯用套路就是

int l,r;//左右区间
int cf[maxn];//差分数组
int a[maxn];//原数组
int val;//要修改的值
cf[l]+=val;
cf[r+1]-=val;
for(int i=1;i<=n;i++)
    a[i]+=cf[i]+cf[i-1];

可简单概括为首加尾减

铺地毯：暴力O（nmk），差分优化后O（kn+nm）

2.啥是乔治树上差分？

刚刚说了lxy：我不是我没有，差分是利用前缀和思想在一个连续区间内，通过单点修改优化区间修改的一种思想，而这又如何在树上实现呢？

树上差分实际又分为边的差分和点的差分两种，差别体现在对lca的处理上

这是树上的两点

已知树的性质有

1.任意两个节点之间有且只有一条路径。

2.一个节点只有一个父亲节点。

可得，u到v的路径有且只有一条，我们可以将其拆为u->lca，lca->v两条路径，分别讨论

先看u->lca

正常差分即可

再看lca->v

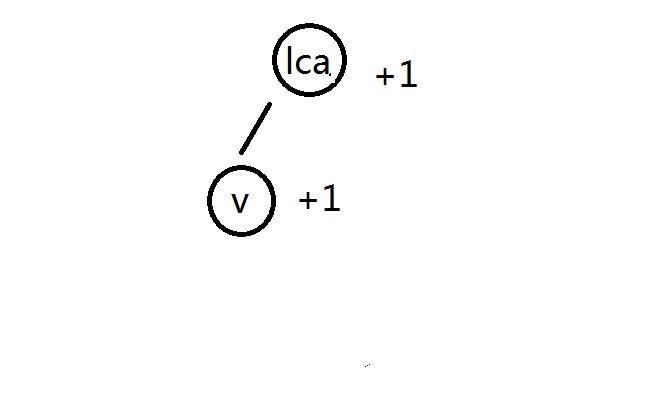
如果是边的差分，那么就不包括lca，将lca上的计数全减去
如果是点的差分，那么就包括lca，不过因为重复算了一次，要删去一次计数

这样差分的复杂度约为O（qlogn），若使用tarjan求lca，logn还能再优化

例题

板子：

Max Flow：

 1 const int maxn=1e6+5;
 2 struct A
 3 {
 4     int v,next;
 5 }e[maxn];
 6 int n,k,tot,ans,head[maxn],sum[maxn],dep[maxn],f[maxn][22],Lca;
 7 void add(int x,int y)
 8 {
 9     e[++tot].v=y;
10     e[tot].next=head[x];
11     head[x]=tot;
12 }
13 void dfs(int x,int fa)
14 {
15     dep[x]=dep[fa]+1;
16     for(int i=head[x];i;i=e[i].next)
17     {
18         int v=e[i].v;
19         if(v==fa)
20             continue;
21         f[v][0]=x;
22         dfs(v,x);
23     }
24 }
25 int lca(int x,int y)
26 {
27     if(dep[x]<dep[y])
28         swap(x,y);
29     for(int j=21;j>=0;j--)
30         if((dep[x]-dep[y])&(1<<j))
31             x=f[x][j];
32     if(x==y)
33         return x;
34     for(int j=21;j>=0;j--)
35         if(f[x][j]!=f[y][j])
36         {
37             x=f[x][j];
38             y=f[y][j];
39         }
40     return f[x][0];
41 }
42 void update(int x,int fa)
43 {
44     for(int i=head[x];i;i=e[i].next)
45     {
46         int v=e[i].v;
47         if(v==fa)
48             continue;
49         update(v,x);
50         sum[x]+=sum[v];
51     }
52 }
53 int main()
54 {
55     input();
56     n=red();
57     k=red();
58     int x,y;
59     for(int i=1;i<n;i++)
60     {
61         x=red();
62         y=red();
63         add(x,y);
64         add(y,x);
65     }
66     dfs(1,1);
67     for(int j=1;j<=21;j++)
68         for(int i=1;i<=n;i++)
69             f[i][j]=f[f[i][j-1]][j-1];
70     for(int i=1;i<=k;i++)
71     {
72         x=red();
73         y=red();
74         Lca=lca(x,y);
75         sum[x]++;
76         sum[y]++; 
77         sum[Lca]--;
78         sum[f[Lca][0]]--;
79     }
80     update(1,1);
81     for(int i=1;i<=n;i++)
82         ans=max(ans,sum[i]);
83     printf("%d",ans);
84     return 0;
85 }

View Code

松鼠的新家：

 1 const int maxn=1e6+5;
 2 struct A
 3 {
 4     int v,next;
 5 }e[maxn];
 6 int n,k,tot,ans,a[maxn],head[maxn],sum[maxn],dep[maxn],f[maxn][22],LCA;
 7 void add(int x,int y)
 8 {
 9     e[++tot].v=y;
10     e[tot].next=head[x];
11     head[x]=tot;
12 }
13 void dfs(int x,int fa)
14 {
15     dep[x]=dep[fa]+1; 
16     for(int i=head[x];i;i=e[i].next)
17     {
18         int v=e[i].v;
19         if(v==fa)
20             continue;
21         f[v][0]=x;
22         dfs(v,x);
23     }
24 }
25 int lca(int x,int y)
26 {
27     if(dep[x]<dep[y])
28         swap(x,y);
29     for(int j=21;j>=0;j--)
30         if((dep[x]-dep[y])&(1<<j))
31             x=f[x][j];
32     if(x==y)
33         return x;
34     for(int j=21;j>=0;j--)
35         if(f[x][j]!=f[y][j])
36         {
37             x=f[x][j];
38             y=f[y][j];
39         }
40     return f[x][0];
41 }
42 void update(int x,int fa)
43 {
44     for(int i=head[x];i;i=e[i].next)
45     {
46         int v=e[i].v;
47         if(v==fa)
48             continue;
49         update(v,x);
50         sum[x]+=sum[v];
51     }
52 }
53 int main()
54 {
55     input();
56     n=red();
57     for(int i=1;i<=n;i++) 
58         a[i]=red();
59     int x,y;
60     for(int i=1;i<n;i++)
61     {
62         x=red();
63         y=red();
64         add(x,y);
65         add(y,x);
66     }
67     dfs(1,1);
68     for(int j=1;j<=21;j++)
69         for(int i=1;i<=n;i++)
70             f[i][j]=f[f[i][j-1]][j-1];
71     for(int i=2;i<=n;i++)
72     {
73         LCA=lca(a[i],a[i-1]);
74         sum[a[i]]++;
75         sum[a[i-1]]++;
76         sum[LCA]--;
77         sum[f[LCA][0]]--;
78     }
79     update(1,1);
80     sum[a[1]]++;
81     for(int i=1;i<=n;i++)
82         printf("%d
",sum[i]-1);
83     return 0;
84 }

View Code

Grass Planting

略有难度：

Alyona and a tree
network
运输计划

还有大家都知道的天天爱跑步：

  1 /*
  2 id:Dear_prince 
  3 */ 
  4 #define INF 1e10
  5 const int maxn=600011;
  6 struct A
  7 {
  8     int v,w,next;
  9 }e[maxn];
 10 struct B
 11 {
 12     int s,t,lca,len;
 13 }p[maxn];
 14 int tot,head[maxn],n,m,w[maxn],vl[maxn],ans[maxn],deep[maxn],f[maxn][21],maxd,t1[maxn],t2[maxn];
 15 vector<int> g[maxn];
 16 vector<int> gg[maxn];
 17 vector<int> ggg[maxn];
 18 void add(int x,int y)
 19 {
 20     e[++tot].v=y;
 21     e[tot].next=head[x];
 22     head[x]=tot;
 23 }
 24 void dfs1(int x,int fa)
 25 {
 26     for(int i=head[x];i;i=e[i].next)
 27     {
 28         int v=e[i].v;
 29         if(v==fa)
 30             continue;
 31         deep[v]=deep[x]+1;
 32         f[v][0]=x;
 33         dfs1(v,x);
 34     }
 35 }
 36 int lca(int x,int y)
 37 {
 38     if(deep[x]<deep[y])
 39         swap(x,y);
 40     int t=0;
 41     while((1<<t)<=deep[x])
 42         t++;
 43     t--;
 44     for(int i=t;i>=0;i--)
 45         if(deep[x]-(1<<i)>=deep[y])
 46             x=f[x][i];
 47     if(x==y)
 48         return x;
 49     for(int i=t;i>=0;i--)
 50     {
 51         if(f[x][i]!=f[y][i])
 52         {
 53             x=f[x][i];
 54             y=f[y][i];
 55         }
 56     }
 57     return f[x][0]; 
 58 }
 59 void dfs2(int x,int fa)
 60 {
 61     int now=w[x]+deep[x];
 62     int cun=0;
 63     if(now<=maxd)
 64         cun=t1[now];
 65     for(int i=head[x];i;i=e[i].next)
 66     {
 67         int v=e[i].v;
 68         if(v==fa)
 69             continue;
 70         dfs2(v,x);
 71     }
 72     t1[deep[x]]+=vl[x];
 73     if(now<=maxd)
 74         ans[x]=t1[now]-cun;
 75     for(int i=0;i<g[x].size();i++)
 76         t1[deep[g[x][i]]]--;
 77 }
 78 void dfs3(int x,int fa)
 79 {
 80     int now=deep[x]-w[x];
 81     now+=300000;
 82     int cun=t2[now];
 83     for(int i=head[x];i;i=e[i].next)
 84     {
 85         int v=e[i].v;
 86         if(v==fa)
 87             continue;
 88         dfs3(v,x);
 89     }
 90     for(int i=0;i<gg[x].size();i++)
 91         t2[300000+gg[x][i]]++;
 92     ans[x]+=t2[now]-cun;
 93     for(int i=0;i<ggg[x].size();i++)
 94         t2[300000+ggg[x][i]]--; 
 95 }
 96 int main()
 97 {
 98     //input();
 99     n=red();
100     m=red();
101     int x,y;
102     for(int i=1;i<n;i++)
103     {
104         x=red();
105         y=red();
106         add(x,y);
107         add(y,x);
108     }
109     for(int i=1;i<=n;i++)
110         w[i]=red();
111     deep[1]=1;
112     dfs1(1,0);
113     for(int i=1;i<=n;i++)
114         maxd=max(maxd,deep[i]); 
115     for(int j=1;j<=19;j++)
116         for(int i=1;i<=n;i++) 
117             f[i][j]=f[f[i][j-1]][j-1];
118     for(int i=1;i<=m;i++)
119     {
120         p[i].s=red();
121         p[i].t=red();
122         vl[p[i].s]++;
123         p[i].lca=lca(p[i].s,p[i].t);
124         p[i].len=deep[p[i].s]+deep[p[i].t]-2*deep[p[i].lca];
125         g[p[i].lca].push_back(p[i].s);
126     }
127     dfs2(1,0);
128     for(int i=1;i<=m;i++)
129     {
130         gg[p[i].t].push_back(deep[p[i].t]-p[i].len);
131         ggg[p[i].lca].push_back(deep[p[i].t]-p[i].len);
132     }
133     dfs3(1,0);
134     for(int i=1;i<=m;i++)
135         if(deep[p[i].s]-deep[p[i].lca]==w[p[i].lca])
136             ans[p[i].lca]--; 
137     for(int i=1;i<=n;i++)
138         printf("%d ",ans[i]);
139     return 0;
140 }

View Code

相关阅读:
『奇葩问题集锦』npm install 报错 node-pre-gyp ERR! node-pre-gyp -v v0.6.25
『奇葩问题集锦』Ruby 切换淘宝源报错WARNING: Error fetching data: SSL_connect returned=1 errno=0 state=SSLv3 read s erver certificate B: certificate verify failed
一分钟搭建Webpack+react+es6框架
 『奇葩问题集锦』Cannot find module 'webpack/lib/node/NodeTemplatePlugin'
『奇葩问题集锦』Zepto 页面唤醒拨号功能点透
 webpack面试题（转载）
手机端样式
 输入框问题
 白色表单隐式边框阴影
 线性渐变css
原文地址：https://www.cnblogs.com/Achensy/p/10414019.html