OO第一单元总结
2019-03-27
一、基于度量分析程序结构
- 第一次作业
由于第一次作业较为简单,在此就简单阐述一下,不放类图了。
结构的设计很简单,整体的考量也十分自然。为每个项建立原子类(这里把运算符也代入成系数的一部分),抽象出每个项的数据特征,即指数和系数(常数项指数为0);需要实现的行为有求导和对象信息输出(toString),设置相应方法。建立多项式类,用LinkedList存储每一个项对象;实现insert方法将项插入构建多项式,其实可以用HashMap,合并同类项时无需遍历搜索(但因为List比较好写,摸了);实现多项式类的求导和输出方法,只需遍历实现每个项的求导和输出方法即可。
优点:
1. 结构简洁清晰(大概也是绝大多数同学采取的类似的架构)
缺点:
1. 其实本应为输入处理专门设置一个类,直接在主函数里处理导致主类复杂度偏高(可能还带着些许面向过程的思想)
2. 采用大正则判断输入合法性(很不为推崇的一种方式但简单……其实应该用小正则分解字符串的),也因此增加了主类的复杂度
3. 关于优化,忘了考虑系数为负的项放首位长度会多一个负号,没有做到最优还是考虑不周
收获:
初步建立了面向对象的思想,掌握了正则表达式的基本使用方法(但未必是正确使用方法)
- 第二次作业
第二次作业的类图基本上是第三次作业的一个子图(因此就不放了),沿袭上一次作业的思想依次构建多项式类、项类、因子类。第一次尝试使用了Factor接口类,定义抽象方法diff和toString;幂函数类、三角函数类实现Factor接口并实现各自的求导和输出方法(常数因子作为项的系数)。项类内部定义一个Factor类数组用于存储构成项的各个因子,相应的求导方法就很好写(只需操纵因子数组而不需要加入一系列特判)。多项式类同样用LinkedList存储每一项。其实这些都还好,主要难点还是在优化(不会优化的抱头痛哭)。
-
- 基于Metrics的复杂度分析



用Metrics简单分析了下程序结构,发现主类复杂度还是严重超标了orz(输入处理全部放主类+大正则屡试不爽的锅),此外多项式类的复杂度也相对偏高,应该是由于在里面放了一些奇奇怪怪的优化方法(现在想来或许应该为优化单独创建一个类,处理起来更为清晰而且方便定位bug,还是太naive)。关于方法复杂度,超标的分别是主方法和优化用的方法1、方法2……(后来事实也的确证明在优化方法中出现了bug)
优点:
1. 对因子采用了接口和多态的机制,使求导操作归一化,程序能有较小程度的延展性
缺点:
1. 同上应该为输入处理专门设置一个类,降低主类复杂度
2. 采用大正则判断输入合法性(硬是用大正则判断合法性,于是第三次作业教你做人 :-))
3. 关于优化,由于能力有限(就是菜),只做到简单的将sin(x)^2+cos(x)^2 = 1合并(本来还想实现将cos(x)^2用1-sin(x)^2替换看看替换后的字符串长度能否缩短,但摸得太过分周二才开始实践,于是果不其然出了各种各样的bug,只好放弃)
收获:
最大的收获应该是用到了接口和多态的机制,对面向对象的概念有了更为深入的了解
- 第三次作业
- 结构

由于本次作业的工程量相比前两次有较大幅度的提升,采用包机制把十几个无序的类进行有序管理(至少看得是真的清晰易懂)。
基于输入处理、递归下降构建表达式树、求导、输出的一系列步骤把要构建的类分为三大块,一是输入的预处理(进行了部分非法格式的判断)。
二是最最重要的也是本次作业的难点所在——递归下降构建表达式树。首先谈谈整体的架构,这部分仍然沿袭上一次作业的思想,定义Factor接口实现四种因子类(常数因子依然作为项的系数出现),一个项内部存有FactorList,而一个表达式内部则存有TermList,这是很自然的一种想法,唯一对理解造成困难的应该是这次新增的表达式因子类,一个表达式可以是表达式,也可以作为因子构成项的一部分?当时纠结了好一段时间,最终还是决定分开考虑:表达式因子就只是因子,只不过内部存了一个表达式 :-),求导的时候也需要额外注意(因为在Factor接口中定义求导方法的返回类型是一个Term)。求导和输出方法的实现与上次作业类同。这样一个表达式树的基本架构就搭建好了。
然后是难度最大的用递归下降处理字符串,为此专门学习了一些编译里的文法知识,也查阅了不少资料(看到头大)。为了方便接下来的处理,第一步是按照网上查到的方法以及讨论区dalao给出的建议划分词法单元,用一个枚举类TokenSign列举了所有可能出现的标识符如下:
1 public enum TokenSign { 2 X, NUM, ADD, SUB, MUL, POW, 3 LPAREN, RPAREN, SIN, COS, ERROR 4 }
其次是在输入串中不断提取分隔Tokens,给出一段识别并建立Token的代码:

1 public Token nextToken(String str) { 2 Token tk = new Token(); 3 tk.setType(TokenSign.ERROR); 4 int i = 0; 5 StringBuilder p = new StringBuilder(""); 6 if (str.charAt(i) == '+') { 7 tk.setType(TokenSign.ADD); 8 tk.setValue("+"); 9 } else if (str.charAt(i) == '-') { 10 tk.setType(TokenSign.SUB); 11 tk.setValue("-"); 12 } else if (str.charAt(i) == '*') { 13 tk.setType(TokenSign.MUL); 14 tk.setValue("*"); 15 } else if (str.charAt(i) == '^') { 16 tk.setType(TokenSign.POW); 17 tk.setValue("^"); 18 } else if (str.charAt(i) == 'x') { 19 tk.setType(TokenSign.X); 20 tk.setValue("x"); 21 } else if (str.charAt(i) == '(') { 22 tk.setType(TokenSign.LPAREN); 23 tk.setValue("("); 24 } else if (str.charAt(i) == ')') { 25 tk.setType(TokenSign.RPAREN); 26 tk.setValue(")"); 27 } 28 if (tk.type != TokenSign.ERROR) { 29 i++; 30 return tk; 31 } 32 if (isDigit(str.charAt(i))) { 33 while (i < str.length() && isDigit(str.charAt(i))) { 34 p.append(str.charAt(i)); 35 i++; 36 } 37 tk.setType(TokenSign.NUM); 38 tk.setValue(p.toString()); 39 return tk; 40 } //get number 41 if (i < str.length() - 2 && str.charAt(i) == 's') { 42 if (str.charAt(i + 1) == 'i' && str.charAt(i + 2) == 'n') { 43 tk.setType(TokenSign.SIN); 44 tk.setValue("sin"); 45 return tk; 46 } 47 } //get sin 48 if (i < str.length() - 2 && str.charAt(i) == 'c') { 49 if (str.charAt(i + 1) == 'o' && str.charAt(i + 2) == 's') { 50 tk.setType(TokenSign.COS); 51 tk.setValue("cos"); 52 return tk; 53 } 54 } 55 return tk; 56 }
其实就是把一整个串划分成更小的字符串单元方便之后进行处理,划分好以后存入TokensList进行递归下降(!!!)重点的递归下降是为表达式类、项类、因子类以及细分的因子类各自构建新的构造函数(说法可能有些不恰当),最终的表现形式跟有限状态机非常相似,通过最开始在expression()读取一个term(),递归调用term()读取factor(),在factor()方法内部判断需要构造的因子类型(这里若是表达式因子则返回到expression()中)。大致的思路如此,真正需要处理的时候需要考虑到很多细节方面的问题(如字符串偏移量的处理需要十分小心、括号匹配等问题)。以及顺便在构建表达式树的过程中判断表达式合法性。一旦构造好后面只需调用表达式类的求导方法一键diff输出即可(
-
- 基于Metrics的复杂度分析


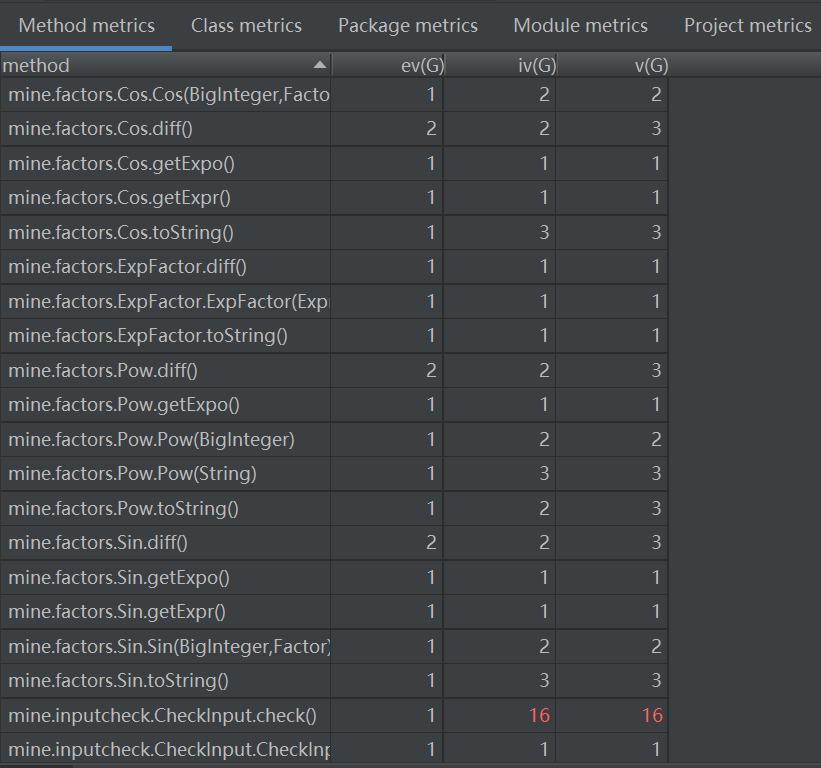
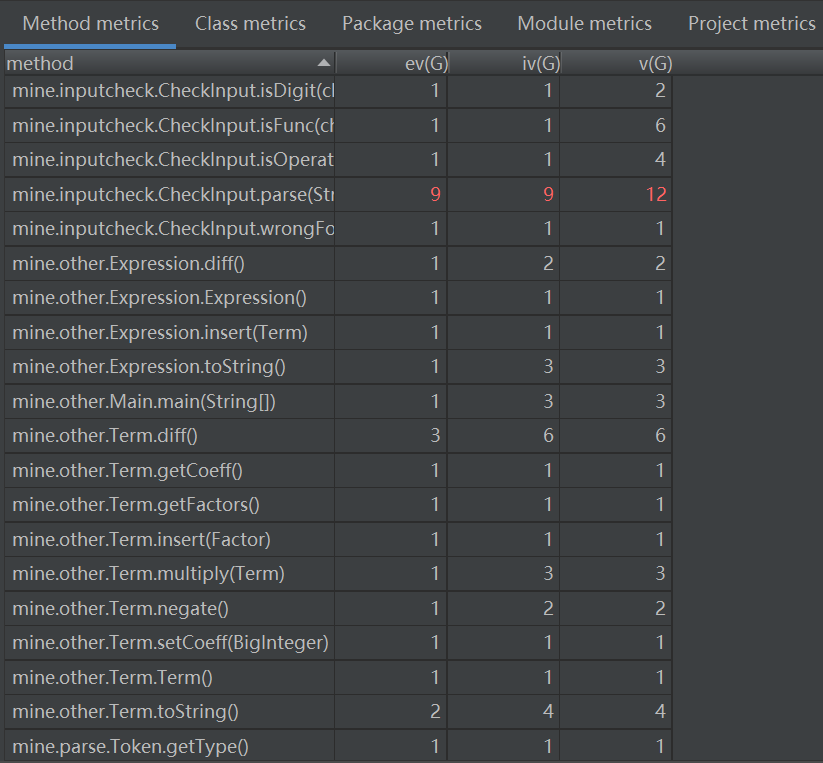
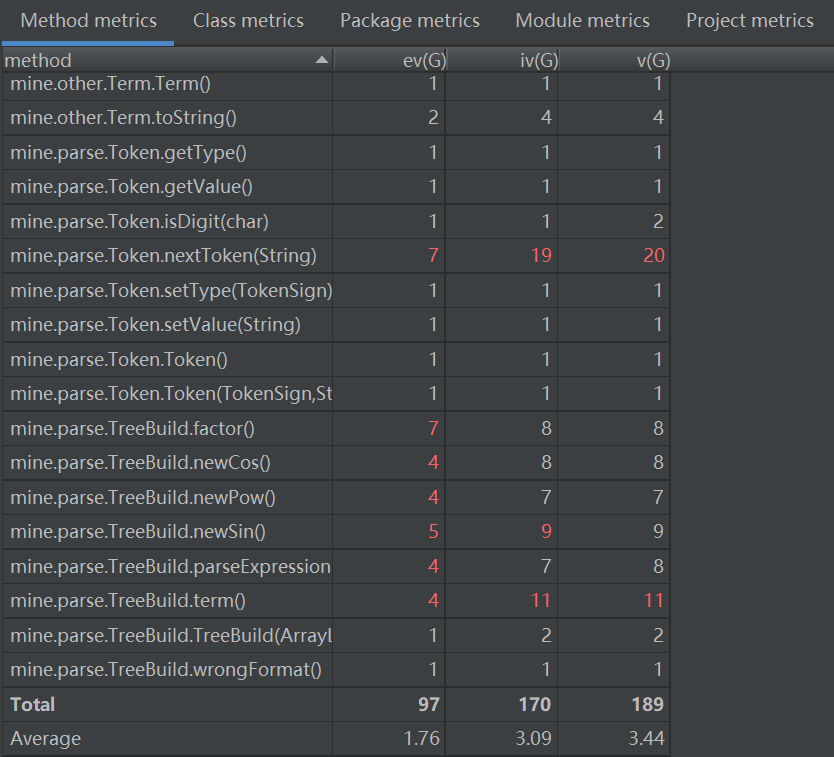
用Metrics分析本次作业后发现自己的输入预处理类和表达式解析构建表达树类的复杂度明显偏高(但似乎可以理解),关于如何处理输入串的类构建上的设计还存在缺陷。关于方法的复杂度,可以看到明显偏高的几个方法都是用于输入预处理和表达式树构建上的(还有一个划分词法单元的方法),说明在相应方法的实现上仍有不足之处。
优点:
1. 利用递归下降处理输入串的构建,较好地解决了表达式因子多层嵌套的问题
2. 大概是第一次掌握了正则的正确用法 :-)
缺点:
1. 由于思虑不周忘记了好几种重要的情况(如指数可以带+、常数因子可以带-、三角函数内带常数因子的情况……等等),虽然强测中侥幸没有测出bug但在互测中就……
2. 关于优化,其实这次能写完整个程序、保证正确性就已经尽力了……优化什么的不敢想了(苦笑.jpg)
收获:
接触到了编译文法方面的相关知识,第一次成功使用了递归下降,对接口与多态的机制有了更深刻的了解
二、关于自己程序的bug
- 强测
在三次强测中,第二次强测出现了bug,原因是做优化时未考虑只有一项指数为负的情况导致出现异常(具体说是为了减少输出长度,若第一项带-号则遍历随后其他项寻找一项带整系数的插到linkedlist的头部,而在实现的时候忽略了若只有一项系数为负的情况,很智障)
事实上第三次强测的数据巧妙地避开了一系列bug(当然这些遗漏的bug在互测中体现得淋漓尽致),主要是由于时间仓促未考虑到一些特殊的情况(如:sin(-1)、sin(++9)等),只能说考虑不周(甚至犯了忘记指数可以带+号这类天大的错误)。
- 互测
在三次互测中都或多或少地被发现了一些bug。
第一次是在处理输出的时候考虑项的数目>1的情况下直接忽略系数为0的项的输出,但疏忽了一个多项式中有多个项全为0的情况,很智障。
第二次犯下的也是类似第一次的考虑不周的问题,在多项式中项的排列处理问题上本来考虑提取一个正项放到List头部,但没考虑所有项系数都为负的情况导致报异常。以上都是细节方面未考虑全导致的bug。
第三次作业没考虑到的情况非常致命,上面也提到了,在互测过程中被hack得有些惨。事实上后来发现我对WF的判断也疏漏了几种特殊情况。综上我的第三次作业中的确充斥着各种各样的漏洞,能活过强测真的只是侥幸(说到这个心情确实有些复杂)
总体来看,这三次作业中写下的bug通常都是在实现时忽略了一些极端、特殊的情况造成的,在写下程序的时候应该三思而后行,或者应该考虑周全后再动手,比起想到什么直接莽出错概率应该会小很多。
三、发现别人程序bug所采用的策略
1.构造测试数据
感谢同学在讨论区给出的java的Xeger包资源,前两次作业都用这个包由正则表达式生成了大量随机的测试数据,可惜的是第三次作业由于存在因子递归嵌套的问题无法直接依据正则表达式生成数据,所以需要自己动脑设计测试用数据。
2.测试bug
很遗憾在前两次作业的时候只会傻瓜式复制粘贴一个个测试,效率不高且耗费了许多时间。第三次有幸得到了同学用python写的对拍程序,测试效率大大提升了几个档次。(讲真,这年头没有个评测姬是不是已经被时代淘汰了……)
3.定位bug
通常在用测试数据发现了对方的bug后会尝试用idea的debug工具定位对方的bug,从而较为清晰地得知对方犯下了何种错误(遇到过正则表达式有误、预处理表达式符号时替换顺序有误(当出现+--型会报异常)、数组越界异常等等)
4.若是仍找不出bug
开启idea自带的debug工具单步运行,体会对方程序的逻辑思路。(很不幸的是,由于个人读代码能力较弱,很少能从观摩对方代码本身发现对方逻辑上存在的漏洞等,不过感受最深的是代码可读性方面的巨大差异)
四、Applying Creational Pattern
第一单元的三次作业是一个逐步递进的过程,后面的作业基本能做到对前面作业向下兼容,可能是因为设计上比较中规中矩大量重构的情况并没有发生,基本都能够在前一次作业的基础上进行扩展(但这个扩展的代码量就有些可观了,特指第二次到第三次)。
关于创建对象的模式,用得最多的还是自定义构造函数的模式,直接用构造函数new一个新对象。后来也了解过工厂模式,实现类加工工厂(即通过一个函数封装创建对象的细节,配合接口使用似乎更佳),工厂模式能成功解决字面创建单个对象而造成大量代码重复的问题(但在这几次作业中我并没有用到)。第三次作业比较特殊,对于表达式对象的创建采取和前两次不同的方法,通过递归下降解析同时生成相应的因子、项和表达式。
五、一点不是感想的感想
- OO的可怕之处已经初步认识到了
- 讨论区应该时刻关注(事实上这几次作业或多或少借鉴了讨论区dalao的经验)
- 遇到理解上的巨大困难的时候不要一直一个人死磕,跟同学交流一番或许会好很多
- 虽然客观上应该先进行详尽的构思设计再写代码,但有时候先动手尝试也不失为一种加深理解的好方法(特指第三次作业,想到脑袋爆炸最终还是在实践的过程中顺带深入理解)
最后,虽然自己很菜,但还是会尽我所能好好学OO的!希望大家一起加油!
附录
1.关于Metrics分析的一些说明
ev(G): 基本复杂度。用来衡量程序非结构化程度,非结构成分降低了程序的质量,增加了代码的维护难度,使程序难于理解。基本复杂度高意味着非结构化程度高,难以模块化和维护。
iv(G): 模块设计复杂度。用来衡量模块判定结构,即模块和其他模块的调用关系。软件模块设计复杂度高意味模块耦合度高,将导致模块难于隔离、维护和复用。
v(G): 圈复杂度。用来衡量一个模块判定结构的复杂程度,数量上表现为独立路径的条数,即合理的预防错误所需测试的最少路径条数。圈复杂度大说明程序代码可能质量低且难于测试和维护。经验表明,程序的可能错误和高的圈复杂度有着很大关系。
OCavg:类的方法的平均循环复杂度。
WMC:类的方法的总循环复杂度。
