今天跟大家聊聊算法复杂性的问题,讲之前我先吐槽一下,这两天我在网上到处搜索关于算法复杂性分析的文章,大多数文章给我的感觉就是看到的第一眼就会吓死初学者……所以我尽可能的利用能让新手理解的语言把这个东西给大家讲明白所以不可避免的会出现,用词不严谨的地方,所以请大家谅解,话不多说,开讲
什么是算法的复杂度
- 算法复杂度即算法所需要的计算机资源
- 算法的复杂度可分为算法的时间复杂度T(n)和算法的空间复杂度S(n),其中n是问题的规模(输入大小)
算法的时间复杂度
时间复杂度就是函数种基本操作所执行的次数,记为T(n),可分为:
- 最坏情况下的时间复杂度
- 最好情况下的时间复杂度
- 平均情况下的时间复杂度
算法的空间复杂度
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的度量,记为S(n),可分为:
- 程序的保存所需要的存储空间资源。即程序的大小
- 程序在执行过程中所需要消耗的存储空间资源,如中间变量等
时间与空间复杂度的联系
一个算法的时间复杂度和空间复杂度往往是相互影响的,追求好的时间复杂度必然要牺牲空间复杂度的性能,而追求好的空间复杂度必然要牺牲时间复杂度的性能。鱼与熊掌不可兼得。
算法的渐近时间复杂度
为了简化复杂性分析我们引入3个渐进意义下的记号:Ο(渐进上界)、Ω(渐进下界)、θ(渐进紧界)****(剩余两个符号我后续会补上)
θ —— 渐进紧界
首先介绍渐进紧界
对于给定的函数g(n)
θ(g(n)) = {f(n)|∃ c1,c2>0, n0,∀* n>n0, c1g(n)≤f(n)≤c2g(n)}***
f(n)∈θ(g(n)),记作f(n)=θ(g(n))
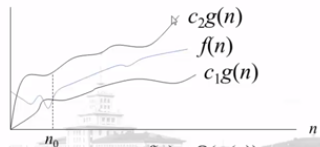
上来看公式相信让好多老铁一下子就退缩了,其实这个公式远比你想的要简单
通俗的讲就是存在c1,c2对于任意一个大于n0的n,使得这个式子成立
c1g(n)≤f(n)≤c2g(n)
Ο —— 渐进上界
对于给定的函数g(n)
O(g(n)) = {f(n):存在正常数c和n0满足对于所有n≥n0,0≤f(n)≤cg(n)}
记作f(n)∈O(g(n)),或简记为f(n)=O(g(n))

Ω —— 渐进下界
对于给定的函数g(n)
Ω(g(n)) = {f(n):存在正常数c和n0,使得对于所有n≥n0,0≤cg(n)<f(n)}
记作f(n)∈Ω(g(n)),或简记为f(n)=Ω(g(n))

相信铁子们看到这里还是感觉云里雾里的,我用一个例题来帮大家理解

(后期持续更新)
联系我
博客园:https://www.cnblogs.com/AWSG-Shaodw/
CSDN:https://blog.csdn.net/AngleWithShotgun/
简书:https://www.jianshu.com/u/df7323cbc116
微信公众号:
