图着色算法详解（Graph Coloring）

图着色算法描述：

https://www.jianshu.com/p/6a52b390f5fa

给定无向连通图和m种不同的颜色。用这些颜色为图G的各顶点着色，每个顶点着一种颜色。是否有一种着色法使G中每条边的两个顶点有不同的颜色。

这个问题是图的m可着色判定问题。若一个图最少需要m种颜色才能使图中每条边相连接的两个顶点着不同颜色，称这个数m为这个图的色数。

求一个图的色数m称为图的m可着色优化问题。 给定一个图以及m种颜色，请计算出涂色方案数。

 

 

分析：

        细致分析后，t代表顶点还是能分析出来的。
　　使用到了邻接矩阵
　　还有就是color数组，也是解题的关键，要明确color数组代表的含义：color[n],大小为n,下标肯定代表顶点，里面的值代表这个顶点放的是哪种颜色。
　　Traceback（t）的t代表某一个顶点，这个顶点具体放哪种颜色不知道，肯定有个for循环从第一种颜色到最后一种颜色都要试一下，那么color[t]里就放当前这种颜色。OK（t）判断一下，如果可以，traceback（t+1）。
　　OK（t）中，t顶点和哪些顶点有联系，我就去判断这些点放置的颜色有没有和我相同，若有相同的，return false;否则，return true。

#include<stdio.h>
#include<iostream>
#define V 4//图中的顶点数
/* 打印解决方案的实用函数 */
void printSolution(int color[])
{
	printf(" Following are the assigned colors 
");
	for (int i = 0; i < V; i++)
		printf(" %d ", color[i]);
	printf("
");
}
bool isSafe(int v, bool graph[V][V], int color[], int c)////用于检查当前颜色分配的实用程序函数
{
	for (int i = 0; i < V; i++)

	if (graph[v][i] && c == color[i])
		return false;
	return true;
}

void graphColoring(bool graph[V][V], int m, int color[], int v)//求解m着色问题的递推效用函数
{

	if (v == V)//基本情况：如果所有顶点都指定了颜色，则返回真
	{
		printSolution(color);
		return;
	}
	/* 考虑这个顶点v并尝试不同的颜色*/
	for (int c = 1; c <= m; c++)
	{
		/* 检查颜色C到V的分配是否正确*/
		if (isSafe(v, graph, color, c))
		{
			color[v] = c;
			/* 递归为其余顶点指定颜色 */
			graphColoring(graph, m, color, v + 1);
			/* 如果指定颜色C不会导致解决方案然后删除它 */
			color[v] = 0;
		}
	}
}
// driver program to test above function
int main()
{
	/* Create following graph and test whether it is 3 colorable
	(3)---(2)
	|   / |
	|  /  |
	| /   |
	(0)---(1)
	*/
	bool graph[V][V] = { { 0, 1, 1, 1 },
	{ 1, 0, 1, 0 },
	{ 1, 1, 0, 1 },
	{ 1, 0, 1, 0 },
	};
	int m = 3; // Number of colors

	int color[V];
	for (int i = 0; i < V; i++)
		color[i] = 0;
	graphColoring(graph, m, color, 0);
	system("pause");
	return 0;
}　　

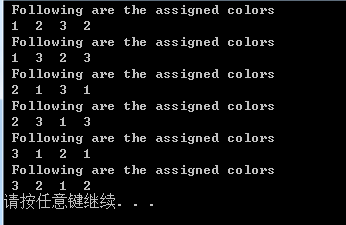
运行结果：