【模板】二分图

---恢复内容开始---

二分图

　　如果一张无向图的N个结点（N>=2）可以分成A，B两个非空集合，其中A∩B为空，并且在同一集合中的点之间没有边相连，那么就称这张图为二分图。A，B被称为二分图的左部和右部。

二分图的判定

　　定理：一张无向图是二分图当且仅当图中不存在奇环（长度为奇数的环）。

　　依据这个定理，我们可以用染色法进行二分图的判定。大致的思想是，我们对所有的点进行黑白染色，使之满足存在边相连的两个点的颜色不相同，依照这样的方法，如果可以把所有的点都染色，那么这张图就一定是二分图，否则这张图就不是二分图。该过程可以基于遍历算法，访问每一个已经确定颜色的点，规定下一次访问的点的颜色如果存在冲突则染色失败，该图不是无向图。

二分图的最大匹配

　　一组匹配指的是”任意两条边都没有公共端点“，而最大匹配指的是一组匹配中存在的边数最多。

　　对于一组匹配S（S是一个边集），属于S的边被称为”匹配边“，不属于S的边称为”非匹配边“。匹配边的端点称为”匹配点“，其他的结点被称为”非匹配结点“。

　　求最大匹配的过程实际上是一个绿与被绿的过程。

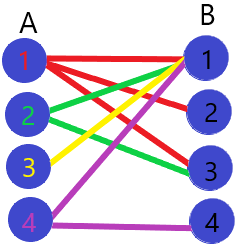
　　对于上图所示的例子，我们依次枚举A组的所有点：

　　对于A1，我们先让他匹配到B1；

　　然后我们考虑A2，A2也想要匹配B1，我们看B1现在的匹配点A1，发现A1还可以匹配B2，所以我们让A1匹配B2，A2匹配B1；

　　接着考虑A3，A3同样想匹配B1，此时B1被A2匹配这，所以我们来看A2，发现A2被还可以去匹配B3，所以我们让A1匹配B2，A2匹配B3，A3匹配B1；

　　最后我们来考虑A4，A4依旧想要匹配B1，而此时的匹配者A3除了B1外没有办法和其他的点匹配，所以A3不会放弃B1，他会让A4去重新寻找匹配点，那么A4就只能退而求其次，以B4作为匹配点；

　　所以A1匹配B2，A2匹配B3，A3匹配B1，A4匹配B4，最大匹配就为4.

　　由上面的算法，我们可以发现最大匹配的思想其实是一个贪心的思想，对于一个A组的点，我们依次考虑他的所有理想匹配点（可以直接到达的点），如果存在一个B组点不属于匹配点集或者可以从匹配点点集中剔除，那么我们就把这个点加入到匹配点集。其中对于如何把一个B组点从匹配点集中剔除，我们可以考略把之前与这个点匹配的A组匹配点给进行二次匹配。

　　用通俗的话来说，如果一个A组的点Ap想要去匹配一个B组的点，那么他有两种选择，一种是去绿一个已经匹配的点Ax，这种行为是存在风险的，如果这个被绿的已匹配点Ax有且只有当前这一种选择时（即他们俩都想匹配的By），那么这个Ap点就匹配失败了；另一种时去找一个没有形成匹配的点匹配。另外我们发现，在可以进行第一种操作的时候，先进行第一种操作失败后再选择第二种操作会更优（不存在增广路）。

模板：洛谷P3386

 #include<bits/stdc++.h>
 using namespace std;
 
 const int MAX = 1005;
 unsigned int Map[MAX][MAX], used[MAX];
 int match[MAX];
 int n, m, e;
  
 bool Dfs(int u)
     {
         for(int v = 1; v <= m; ++ v)
             if(Map[u][v] && !used[v])
                 {
                     used[v] = 1;
                     if(!match[v] || Dfs(match[v]))
                         {
                             match[v] = u;
                             return true;
                         }
                 }
         return false;
      } 
 
 int main()
 {
 //    freopen("test1.in", "r", stdin);
     int x, y;
     scanf("%d%d%d", &n, &m, &e);
     for(int i = 1; i <= e; ++ i)
         {
             scanf("%d%d", &x, &y);
             Map[x][y] = 1;
         }
     int ans = 0;
     for(int i = 1; i <= n; ++ i)
         {
             memset(used, 0, sizeof(used));
             if(Dfs(i)) ans ++;
         }
     printf("%d
", ans);
 }

二分图的最小点覆盖

　　给定一张二分图，求出一个最小点集S，使得图中的任意一条边都至少有一个属于S的端点，这个问题被称为是二分图的最小点覆盖。

　　定理：二分图的最小点覆盖包含的点数等于二分图的最大匹配包含的边数。

二分图的的最大独立集

　　　给定一张无向图G=（V，E），满足下列条件的点集S被称为图的独立集：

1. S是V的子集
2. 任意的x，y属于S都不存在x到y直接相连的边

　　　定理：设G是有n个结点的二分图，G的最大独立集的大小等于n减去最大匹配数。

　　无向图G 的最大团等于其补图的最大独立集。