康托展开:康托展开是一个全排列到一个自然数的双射,常用于构建hash表时的空间压缩。设有n个数(1,2,3,4,…,n),可以有组成不同(n!种)的排列组合,康托展开表示的就是是当前排列组合在n个不同元素的全排列中的名次。
公式:X=a[n]*(n-1)!+a[n-1]*(n-2)!+...+a[i]*(i-1)!+...+a[1]*0!
例如:123的全排列及其康托展开
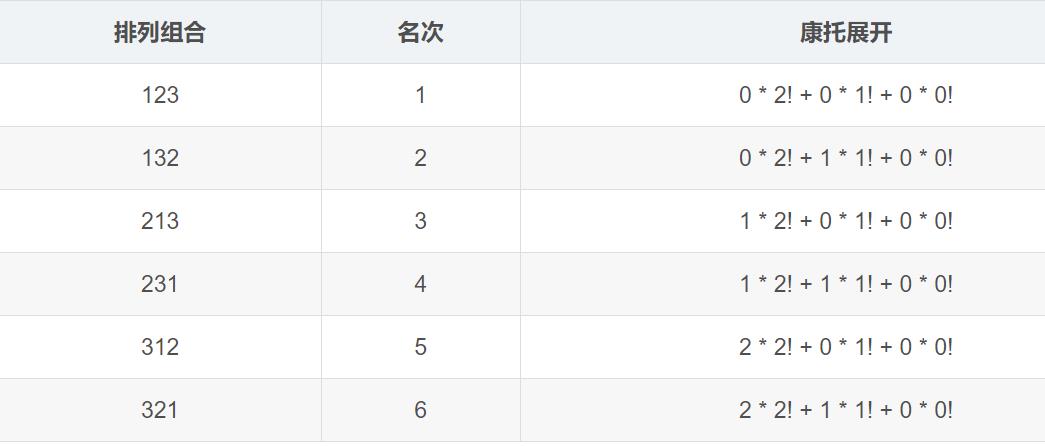
每个康拓值对应着这个排列在全排列中的位置。
代码实现:
int zz[50]={1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880} ;//假设n小于10 int cnator(int* a,int n) { int smaller=0,x=0; for(int i=0;i<n;i++) { smaller=0; for(int j=i+1;j<n;j++) { if(a[j]<a[i]) smaller++; } x+=zz[n-i+1]*smaller; } return x; }
逆康托展开
思路:对于(1,2,3,4,5)给出61(它的康托展开是(3,4,1,5,2))。
61对4! %得13;/得2;所以a[5]=2,比第五位小的数有两个,所以第一位是3;
13对3! %得1;/得2;所以a[4]=1,比第四位小的数有一个,所以第二位是4;
1对2! %得1;/得0;所以a[3]=0,比第三位小的数有0个,所以第三位是1;
1对1! %得0;/得1;所以a[2]=1,比5第二位小的数有1个,所以第四位是5;
最后只剩2;
所以得到结果(3,4,1,5,2);
代码实现:
int zz[50]={1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880}; void decantor(int x,int n) { int i,r,t; vector <int> v,a; for(i=1;i<=n;i++) v.push_back(i); for(i=n;i>=1;i--) { r=x%zz[i-1]; t=x/zz[i-1]; x=r; sort(v.begin(),v.end()); a.push_back(v[t]); v.erase(v.begin()+t); } }
参考文章:https://blog.csdn.net/wbin233/article/details/72998375