前言
分布式算法中经常使用梯度信息来进行优化,一阶方法有:SGD、加速SGD、方差减少SGD、随机坐标减少、双坐标提升方法。这些方法减少了本地计算,但同时需要更多迭代次数和更多的通信量。
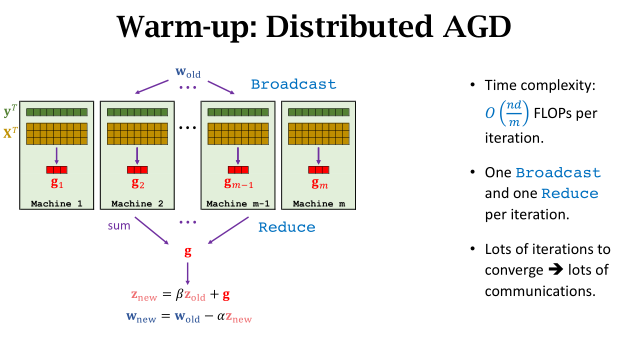
Summary
-
- For big-data problems, distributed optimization is very useful.
-
- If the network is slow, then communication is the bottleneck.
Cost ≈ Computation + Communication
Motivation
-
- Let worker machines do lots of local computations.
-
- Communicate as few as possible.
现在communication-efficient 二阶方法有:AIDE、DANE、CoCoA,他们的共同特征就是利用曲线信息来减少迭代次数和通信时间。论文中使用了牛顿法。
1.Gradient and Hessian(海赛矩阵)

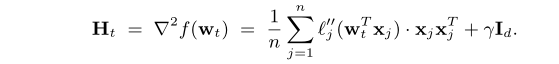
为了计算精确的Hessian,驱动程序通过一次Reduce操作来聚合m个Hessian matrices(每个大小为d*d),通信复杂度为 ,论文中的方法仅需
,论文中的方法仅需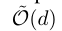 通信复杂度。
通信复杂度。
2.Approximate NewTon (ANT) Directions
每个worker使用本地数据生成一个local Hessian matrix:
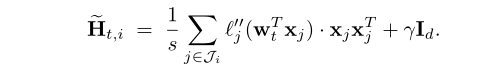
(s为每个worker的随机样本数量,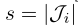 )
)
ANT direction为: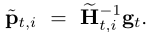
用该方法计算,需要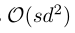 时间构建一个d*d的稠密矩阵并需要
时间构建一个d*d的稠密矩阵并需要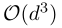 时间去转化。
时间去转化。
为了减少计算成本,我们采用共轭梯度算法(CG)来计算ANT方向:
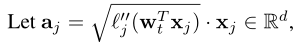
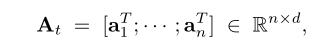
此时,本地 Hessian matrix为:
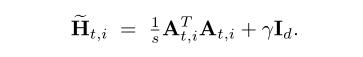
ANT方向为:
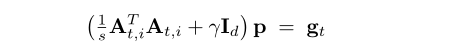
3.Globally Improved ANT (GIANT) Direction
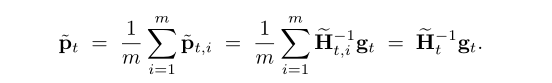
区别在于:
调和平均: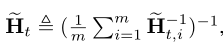
算术平均: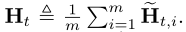 (the true Hessian)
(the true Hessian)
如果数据是散列的,调和平均和算术平均非常接近。计算算术平均需要计算d*d的矩阵,而我们的调和平均只需要计算d维向量。
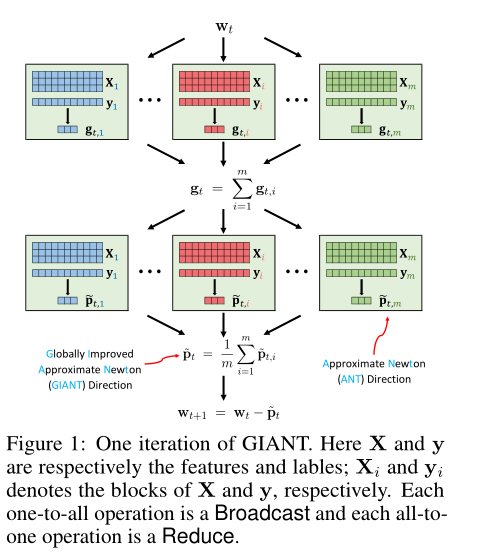
aux information
共轭梯度法(Conjugate Gradient)
共轭梯度法(CG)是介于最速下降法与牛顿法之间的一个方法,它仅需利用一阶导数信息,但克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。 在各种优化算法中,共轭梯度法是非常重要的一种。其优点是所需存储量小,具有步收敛性,稳定性高,而且不需要任何外来参数.
牛顿法

牛顿法 vs 梯度下降法:
从本质上去看,牛顿法是二阶收敛,梯度下降是一阶收敛,所以牛顿法就更快。如果更通俗地说的话,比如你想找一条最短的路径走到一个盆地的最底部,梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步,牛顿法在选择方向时,不仅会考虑坡度是否够大,还会考虑你走了一步之后,坡度是否会变得更大。所以,可以说牛顿法比梯度下降法看得更远一点,能更快地走到最底部。(牛顿法目光更加长远,所以少走弯路;相对而言,梯度下降法只考虑了局部的最优,没有全局思想。)
根据wiki上的解释,从几何上说,牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面,而梯度下降法是用一个平面去拟合当前的局部曲面,通常情况下,二次曲面的拟合会比平面更好,所以牛顿法选择的下降路径会更符合真实的最优下降路径。
牛顿法的优缺点总结:
-
优点:二阶收敛,收敛速度快;
-
缺点:牛顿法是一种迭代算法,每一步都需要求解目标函数的Hessian矩阵的逆矩阵,计算比较复杂。
调和平均数vs算术平均数:https://blog.csdn.net/qixinlei/article/details/98184316?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task
优秀博客:https://www.cnblogs.com/shixiangwan/p/7532830.html
ppt链接:http://wangshusen.github.io/slides/2017-GIANT.pdf