1.在第一章的末尾,有这样的语句。当你和朋友最终熟记了莫尔斯编码之后,可以在口语中使用它,用来取代正常的语言。文字也可以用同样的方式简化成“点”和“划”的序列,莫尔斯编码的口语版把讲话内容缩减到只剩下两个声音了;
2.所以问题的关键就在于数字2。两种闪烁,两种声音。事实上,两个不同的事物,只要经过适当的组合,就可以表示所有的类型的信息,这的确是千真万确的。
=======================================================================================================================================
引出两个不同的事物,亦二进制,嘿嘿
=======================================================================================================================================
3.比起发送莫尔斯码,接收编码并进行解码要费时费力得多,因为译码者不得不根据一串由“点”、“划”组成的晦涩的编码序列来反查字母。
4.问题就出在这里,因为我们现在只有一张提供“字母-莫尔斯码”的编码表,而缺少一张可以显示反向查询的“莫尔斯码-字母”译码表。在开始学习莫尔斯码的初级阶段,如果有这样的一个表无疑将是很方便的。
5.所以忘掉字幕序列吧。或许根据编码中所包含点、划的多少来对其进行分组,是一个更好的组织这些编码的方法;
=======================================================================================================================================
从发送莫尔斯编码到接收莫尔斯编码
=======================================================================================================================================
6.如果知道了莫尔斯编码字中“点”和“划”的数目,那么以这个数目为指数的2的幂运算结果就是其总共可以表示的码字数。

其实,“点”和“划”就是这两种符合的积累组合;
这张图给出了所有字母及其所对应的由“点”和“划”组成的连续序列。
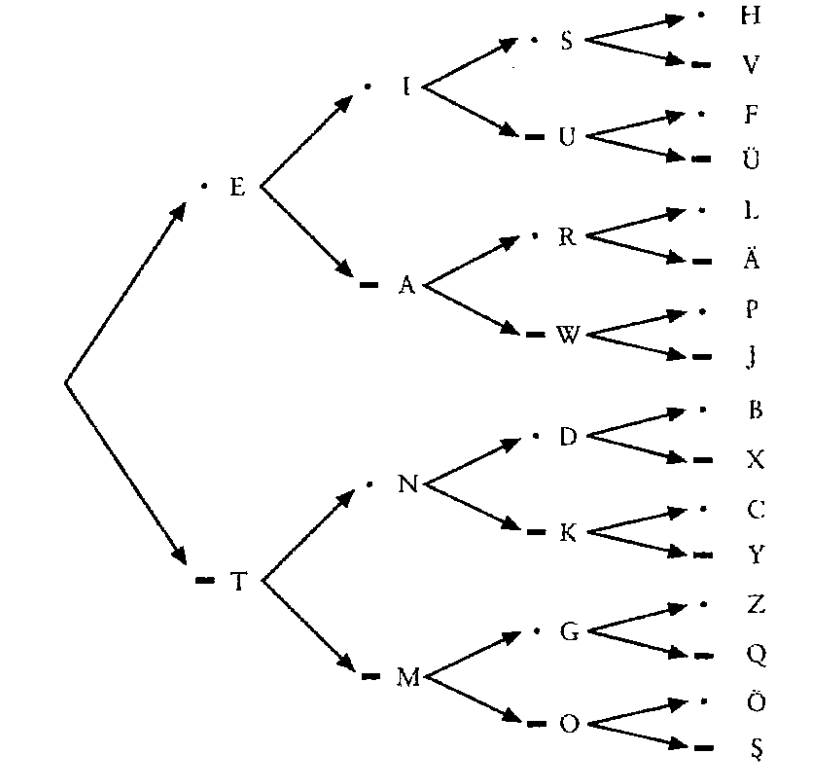
7.当对一串码字进行解码时,我们需要沿着箭头从左向右进行搜寻。
=======================================================================================================================================
所以莫尔斯码也被称作二进制码,因为这种编码的组成元素只有两个--“点”和“划”
传统意义上来说,因为组合分析涉及类似像扔硬币、掷筛子这样的需要对其组合数目进行推算的问题,所以它经常被应用到概率和统计学中。
=======================================================================================================================================
结束,“点”和“划”的组合来计数,引出二进制