题意：
其中，(f(1)=1,f(2)=1)。
传送门
分析：
首先先看斐波那契数列的几何意义：
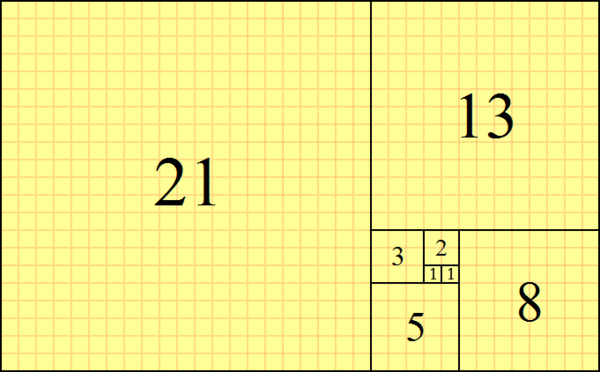图中各数字为正方形的边长。
可以发现其面积关系刚好满足题目中的等式：
(sum_{i=1}^{n}{f(i)}=f(n) imes f(n+1))
因此 (f(n)) 实际上就是斐波那契数列，所以当 (x) 是斐波那契数时，求 (m) 进制下末尾 $0$ 的个数。否则，求 (z) 皇后数（可以预处理出）。
代码：
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int maxn=90;
int a[14]={-1, 1, 0, 0, 2, 10, 4, 40, 92, 352, 724, 2680, 14200, 73712};//n皇后前几项
set<ll>st;
ll num[10],e[10];
void init()
{
ll a=1,b=1,c;
st.insert(1LL);
for(int i=1;i<=maxn;i++)
{
c=a+b;//cout<<"c="<<c<<endl;
a=b;
b=c;
st.insert(c);
}
}
ll divide(ll n)
{
ll cnt=0;
for(ll i=2;i*i<=n;i++)
{
if(n%i==0)
{
num[++cnt]=i;
e[cnt]=0;
while(n%i==0)
{
e[cnt]++;
n/=i;
}
}
}
if(n>1)
{
num[++cnt]=n;
e[cnt]=1;
}
return cnt;
}
ll ct(ll x,ll p)
{
ll cnt=0;
while(x)
{
cnt+=(x/p);
x/=p;
}
return cnt;
}
int main()
{
ll x,m;
init();
scanf("%lld%lld",&x,&m);
if(st.count(x))//是斐波那契数列
{
ll cnt=divide(m);
ll minn=1e18;//要足够大，小了会WA,注意是求阶乘后面的0的个数
for(ll i=1;i<=cnt;i++)
{
ll t=ct(x,num[i]);
minn=min(t/e[i],minn);
}
printf("%lld
",minn);
}
else
{
ll z=(x%min(13*1LL,m))+1;
printf("%d
",a[z]);
}
return 0;
}