Codeforces Round #620 (Div. 2) D

 

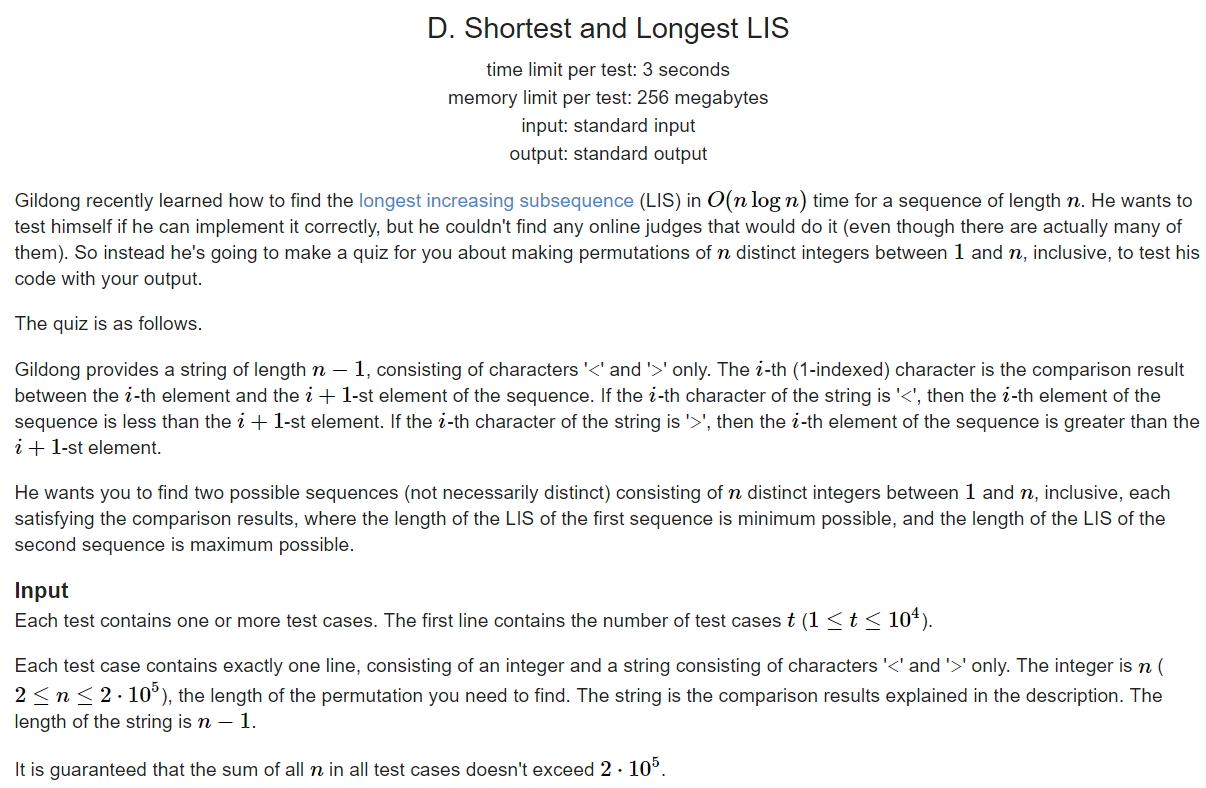
构造一个排列，要求相邻之间的数满足给定的大小关系，然后构造出两个序列，一个序列是所有可能的序列中LIS最长的，一个所有可能的序列中LIS最短的

最短的构造方法：我们考虑所有单调递增的部分，可以发现要让他LIS最小那么就必须要让每一个部分满足前面的比后面的大

最长的构造方法：考虑单调递减的部分，每一个部分都只能选择一个，因此我们要满足后面的部分的值都比前面的大

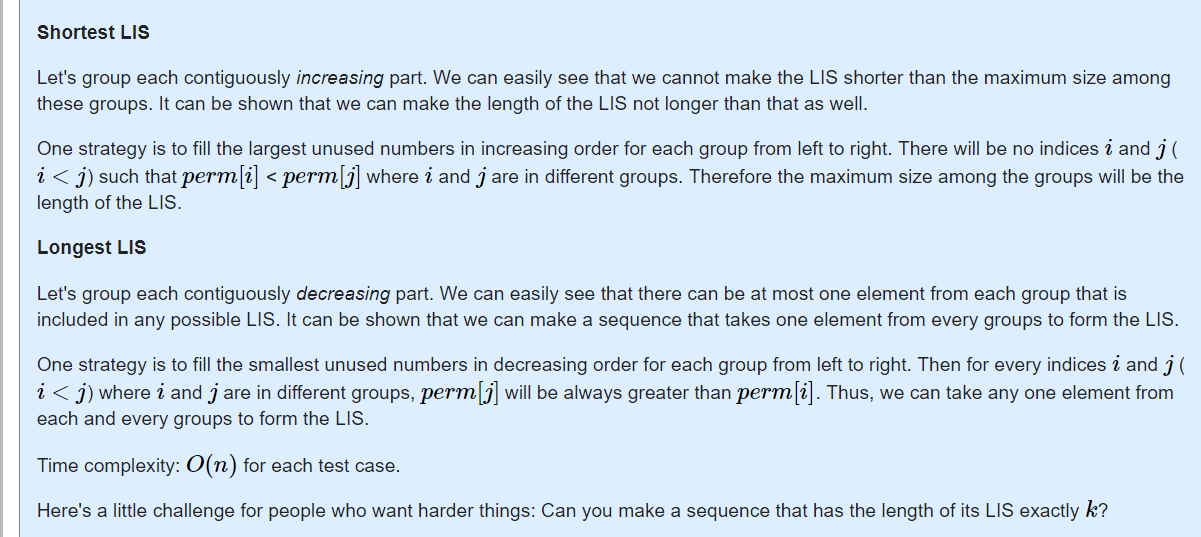
 代码是官方题解的，自己写了半天写不出来

#include <bits/stdc++.h>
using namespace std;

const int MAX_N = 200000;
int ans[MAX_N + 5];

int main()
{
	int tc;
	cin >> tc;
	while (tc--)
	{
		int n, i, j;
		string s;
		cin >> n >> s;

		int num = n, last = 0;
		for (i = 0; i < n; i++)
		{
			if (i == n - 1 || s[i] == '>')
			{
				for (j = i; j >= last; j--)
					ans[j] = num--;
				last = i + 1;
			}
		}
		for (i = 0; i < n; i++)
			cout << ans[i] << (i == n - 1 ? '
' : ' ');

		num = 1, last = 0;
		for (i = 0; i < n; i++)
		{
			if (i == n - 1 || s[i] == '<')
			{
				for (j = i; j >= last; j--)
					ans[j] = num++;
				last = i + 1;
			}
		}
		for (i = 0; i < n; i++)
			cout << ans[i] << (i == n - 1 ? '
' : ' ');
	}
}