各种排序算法的实现、总结

      1.    排序算法

•     比较排序 

      

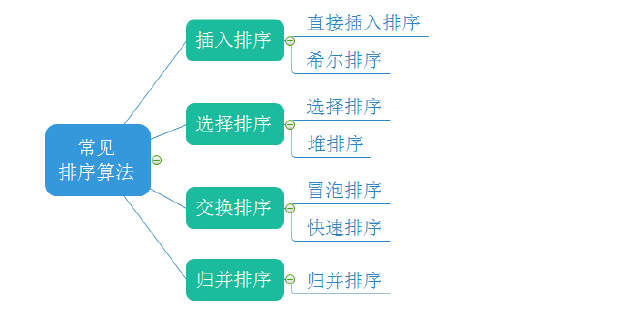
•     非比较排序 

       计数排序、基数排序

     2.    排序算法的实现

        假定序列array[10]={73,22,93,43,55,14,28,65,39,81}  (以升序为例)

•    直接插入排序

直接插入排序就是每一步都将一个待排数据按其大小插入到已经排序的数据中的适当位置，直到全部插入完毕。

void Insertsort(int* array,size_t n)
{
    assert(array);
    for (size_t i = 0; i < n-1; i++)
    {
        int end = i;
        int temp = array[end+1];
        while (end >= 0 && array[end]>temp)
        {
            array[end + 1] = array[end];
            --end;
        }
        array[end + 1] = temp;
    }
}

•        希尔排序

      希尔排序（ShellSort）又称为“缩小增量排序”。该方法的基本思想是：先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接

   插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。

void Shellsort(int* array, size_t n)
{
    assert(array);
    int gap = n;
    while (gap > 1)
    {
        gap = gap / 3 + 1;
        for (size_t i = 0; i < n - gap; i++)
        {
            int end = i;
            int temp = array[end + gap];
            while (end>=0 && array[end] > temp)
            {
                array[end + gap] = array[end];
                end -= gap;
            }
            array[end + gap] = temp;
        }
    }
}

•         选择排序

    选择排序(Selectsort)是一种简单直观的排序算法。它的工作原理如下。首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中   继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

    void Selectsort( int *array, int n)  
    {  
         int i, j, min, temp;  
        for( i = 0; i < n - 1; i ++)  
        {  
            min = i;  
            //查找最小值  
            for( j = i + 1; j < n; j ++)  
                if( array[ min] > array[ j])  
               {
                    min = j; 
             }
            if( min != i)  
            {  
                temp = array[ min];  
                array[ min] = array[ i];  
                array[ i] = temp;  
            }  
        }  
    }  

    简单选择排序算法改进

传统的简单选择排序,每趟循环只能确定一个元素排序后的定位。我们可以考虑改进为每趟循环确定两个元素(当前趟最大和最小记录)的位置,从而减少排序所需的循环次数。

改进后对n个数据进行排序,最多只需进行[n/2]趟循环即可。

void Selectsort_op(int *array, int size)
{
    assert(array);
    int left = 0, right = size - 1;
    while (left < right)
    {
        int minindex = left;
        int maxindex = right;
        for (int i = left; i <= right; i++)
        {
            if (array[i] <= array[minindex])
            {
                minindex = i;
            }
            if (array[i]>array[maxindex])
            {
                maxindex = i;
            }
        }
            swap(array[minindex], array[left]);
            if (maxindex == left)
            {
                maxindex = minindex;
            }
            swap(array[maxindex], array[right]); 
          ++left;
          --right;
    }
}

•       堆排序

     我们的堆排序算法就是抓住了堆的这一特点，每次都取堆顶的元素，将其放在序列最后面，然后将剩余的元素重新调整为最大堆，依次类推，最终得到排序的序列。

  

void _Adjustdown(int* array, int root, size_t size)
{
    assert(array);
    int child = root * 2 + 1;
    while (child < size)
    {
        if (child + 1 < size&&array[child + 1] > array[child])
        {
            child++;
        }
        if (array[child]>array[root])
        {
            swap(array[child], array[root]);
            root = child;
            child = root * 2 + 1;
        }
        else
            break;
    }
}
void Heapsort(int* array,size_t size )
{
    assert(array);
    //建堆(大堆)
    for (int i = (size - 2)/2; i >= 0; i--)
    {
        _Adjustdown(array, i, size);
    }
    //数据调整
    while (--size)
    {
        swap(array[0], array[size]);
        _Adjustdown(array,0, size);
    }
}

•      冒泡排序

     冒泡排序（Bubble Sort）是一种简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。

走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。(设置一个标志位，判断一次循环便利后是否有发生变换的)

void Bubblesort(int * array, size_t size)
{
    assert(array);
    int flag = 0;
    for (size_t end = size - 1; end >= 0; end--)
    {      flag = 0;
        for (size_t ibegin = 0; ibegin < end; ibegin++)
        {   
            if (array[ibegin + 1] < array[ibegin])
            {
                swap(array[ibegin + 1], array[ibegin]);
                flag = 1;
            }
         }
        if (flag == 0)
        {
            break;
        }
    }
}

•     快速排序

         选择数列尾元素，称为 "基准"（key），重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。

在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

递归三种实现方式、两种优化。

优化1：三平取中法

它使得最坏情况发生的几率减小了。

优化2：根据分区大小调整算法

减少递归栈使用的优化，快速排序的实现需要消耗递归栈的空间，而大多数情况下都会通过使用系统递归栈来完成递归求解。

当数据集较小时，不必继续递归调用快速排序算法，使用插入排序代替快速排序。

int Partsort1(int *array, int left, int right)
{
    int key = array[right];
    int begin = left;
    int end = right - 1;
    while (begin <end)
    {
        //找大
        while (begin < end&&array[begin] <= key)
        {
            ++begin;
        }
        //找小
        while (begin<end&&array[end]>key)
        {
            --end;
        }
        if (begin <end)
        {
            swap(array[begin], array[end]);
        }
        if (array[begin]>array[right])
        {
            swap(array[begin], array[right]);
            return begin;
        }
    }
    return right;
}
//快速排序
int Partsort2(int *array, int left, int right)
{
    assert(array);
    int key = array[right];
    int begin = left;
    int end = right;
    while (begin < end)
    {
        while (begin < end&&array[begin] <= key)
        {
            ++begin;
        }
        if (begin < end)
        {
            array[end] = array[begin];
        }
        while (begin < end&&array[end] >= key)
        {
            --end;
        }
        if (begin < end)
        {
            array[begin] = array[end];
        }
    }
    array[begin] = key;
    return begin;

}
//三数取中法
int FindMidPoint(int left,int mid,int right)
{
    if (left <= mid&&left <= right)
    {
        if (mid <= right)
            return mid;
        else
            return right;
    }
    else if (mid <= left&&mid <= right)
    {
        if (left >= right)
            return right;
        else
            return left;
    }
    else
    {
        if (left <= mid)
            return left;
        else
            return mid;
    }
}
//快速排序
int Partsort3(int *array, int left, int right)
{
    assert(array);
    int mid = (right - left) / 2 + left;
    int ret=FindMidPoint(left, mid, right);
    swap(array[ret], array[right]);
    int key = array[right];
    int prev = left - 1;
    int cur = left;
    while (cur < right)
    {
        if (array[cur] < key&& ++prev != cur)
        {
            swap(array[cur], array[prev]);
        }
        ++cur;
    }
    swap(array[++prev], array[right]);
    return prev;
}

void Quicksort(int *array, int left,int right)
{
    assert(array);
    if (left >= right)
    {
        return;
    }
    if (right - left < 16)
    {
        Insertsort(array + left, right - left + 1);
        
    }
    int div = Partsort3(array, left, right);
    Quicksort(array, left, div - 1);
    Quicksort(array, div + 1, right);

}

   非递归实现

#include<stack>
void Quicksort_NonR(int *array, int left, int right)
{
    assert(array);
    stack<int> s;
    s.push(right);
    s.push(left);
    while (!s.empty())
    {
        int begin = s.top();
        s.pop();
        int end = s.top();
        s.pop();
        int div = Partsort3(array, begin, end);
        if (begin < div - 1)
        {
            s.push(div - 1);
            s.push(begin);
        }
        if (div + 1 < end)
        {
            s.push(end);
            s.push(div + 1);
        }
    }
    
}

•        归并排序

        归并排序（Mergesort）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法的一个非常典型的应用。

              把长度为n的输入序列分成两个长度为n/2的子序列。

              对这两个子序列分别采用归并排序。

             将两个排序好的子序列合并成一个最终的排序序列。

             在描述归并排序的步骤时又调用了归并排序本身，可见这是一个递归的过程。

     

void _Merge(int* array, int *tmp, int begin1, int end1,int begin2,int end2)
{
    int index = begin1;
    while (begin1 <= end1&&begin2 <= end2)
    {
        if (array[begin1] < array[begin2])
        {
            tmp[index++] = array[begin1++];
        }
        else
        {
            tmp[index++] = array[begin2++];
        }
    }
    while (begin1 <= end1)
    {
        tmp[index++] = array[begin1++];
    }
    while (begin2 <= end2)
    {
        tmp[index++] = array[begin2++];
    }
}
void _Mergesort(int *array, int *tmp, int left, int right)
{
    if (left < right)
    {
        int mid = left + (right - left) / 2;
        _Mergesort(array, tmp, left, mid);
        _Mergesort(array, tmp, mid+1, right);
        _Merge(array, tmp, left,mid, mid + 1, right);
        memcpy(array + left, tmp + left, sizeof(int)*(right - left + 1));
    }
}
void Mergesort(int *array, size_t n)
{
    assert(array);
    int *tmp = new int[n];
    _Mergesort(array, tmp, 0, n - 1);
    delete[] tmp;
}

•     计数排序

       计数排序算法的步骤：

　　 找出待排序的数组中最大和最小的元素

　　 统计数组中每个值为i的元素出现的次数存入数组Count的第i项

　　反向填充目标数组：将每个元素i放在新数组的第Count(i)项，每 放一个元素就将Count(i)减去1

void Countsort(int *array, size_t n)
{
    assert(array);
    int min = array[0], max = array[0];
    for (size_t i = 1; i < n; i++)
    {
        if (array[i] <= min)
            min = array[i];
        if (array[i] >= max)
            max = array[i];
    }
    int *Count = new int[max - min + 1];
    memset(Count, 0, sizeof(int)*(max - min +1));
    for (int i = 0; i < n; i++)
    {
        Count[array[i] - min]++;
    }
    size_t index = 0;
    for (size_t i = 0; i < max - min + 1; i++)
    {
        while (Count[i]--)
        {
            array[index++] = i + min;
        }
    }
}

•     基数排序

 

   

   

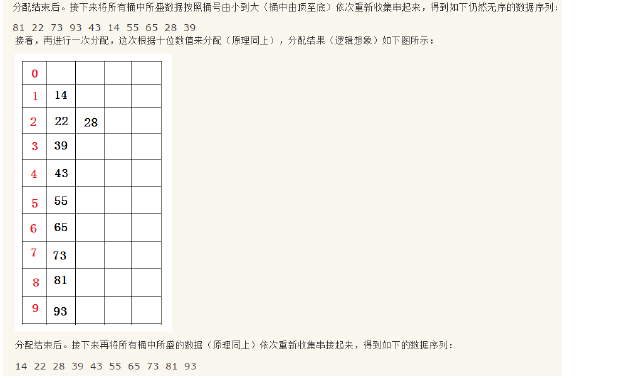
int  GetMaxDigit(int *array, size_t n)
{
    int base = 10;
    int digit = 1;
    for (size_t i = 10; i < n; i++)
    {
        while (array[i] >= base)
        {
            ++digit;
            base *= 10;
        }
    }
    return digit;
}
void LSDsort(int *array, size_t n)
{
    assert(array);
    int count[10] = {0};
    int start[10] = {0};
    int *bucket = new int[10];
    memset(bucket, 0, sizeof(int)*n);
    int maxDigit = GetMaxDigit(array, n);
    int digit = 1;
    int base = 1;
    while (digit <= maxDigit)
    {
        memset(count, 0, sizeof(int)* 10);
        //统计位为0~9数据段
        for (size_t i = 0; i < n; i++)
        {
            int num = (array[i] / base) % 10;
            count[num]++;
        }
        //计算在桶里的起始位置
        start[0] = 0;
        for (int i = 1; i < 10; i++)
        {
            start[i] = start[i - 1] + count[i - 1];
        }
        for (size_t i = 0; i < n; i++)
        {
            int num = (array[i] / base) % 10;
            bucket[start[num]++] = array[i];
        }
        memcpy(array, bucket, sizeof(int)*n);
        base *= 10;
        ++digit;
        delete[] bucket;
   }
}

  3.    排序算法的总结