The cinema theater hall in Sereja's city is n seats lined up in front of one large screen. There are slots for personal possessions to the left and to the right of each seat. Any two adjacent seats have exactly one shared slot. The figure below shows the arrangement of seats and slots for n = 4.
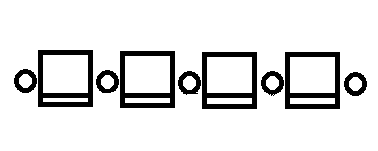
Today it's the premiere of a movie called "Dry Hard". The tickets for all the seats have been sold. There is a very strict controller at the entrance to the theater, so all n people will come into the hall one by one. As soon as a person enters a cinema hall, he immediately (momentarily) takes his seat and occupies all empty slots to the left and to the right from him. If there are no empty slots, the man gets really upset and leaves.
People are not very constant, so it's hard to predict the order in which the viewers will enter the hall. For some seats, Sereja knows the number of the viewer (his number in the entering queue of the viewers) that will come and take this seat. For others, it can be any order.
Being a programmer and a mathematician, Sereja wonders: how many ways are there for the people to enter the hall, such that nobody gets upset? As the number can be quite large, print it modulo 1000000007 (109 + 7).
The first line contains integer n (1 ≤ n ≤ 105). The second line contains n integers, the i-th integer shows either the index of the person (index in the entering queue) with the ticket for the i-th seat or a 0, if his index is not known. It is guaranteed that all positive numbers in the second line are distinct.
You can assume that the index of the person who enters the cinema hall is a unique integer from 1 to n. The person who has index 1 comes first to the hall, the person who has index 2 comes second and so on.
In a single line print the remainder after dividing the answer by number 1000000007 (109 + 7).
11
0 0 0 0 0 0 0 0 0 0 0
1024
6
0 3 1 0 0 0
3
给出一个数n还有n个数ci
如果ci>0,表示排列上的第ci个位置上的数为i
如果ci=0,表示排列上的第ci个位置上的数不确定
即是说,有一个n的排列,其中部分position上的数固定,求有多少种排列满足:
对于排列上的任意一个数x,在x之前不同时存在x+1和x-1这2个数的方案数
solution:
这道题主要在于分情况讨论,得到答案
只要发现一个性质,就可以解决问题了
要保证对于任意一个数x,x+1和x-1不同时存在,则x之前的数放在一起刚好是一个[1,n]的子
区间[L,R],这个自区间的长度为x-1,且有is[x] = L - 1 || is[x] = R + 1
这样我们只需要分情况讨论,
部分情况直接推出公式得到答案
部分情况需要用到递推,同时维护当前的L,R
具体看代码
is[i]表示排列的第i个数固定为is[i]
pre[i]表示第i个数前一个被固定的数,没有则为-1
next[i]表示第i个数后一个被固定的数,没有则为-1
f[i]表示当前考虑到排列的第i个数,当前可行的方案数
ps:
这道题初始化f的时候要注意细节,分情况初始化
//File Name: cf380D.cpp //Author: long //Mail: 736726758@qq.com //Created Time: 2016年05月20日 星期五 00时32分29秒 #include <stdio.h> #include <iostream> #include <algorithm> #include <string.h> #include <stdlib.h> #include <math.h> #include <map> #define LL long long #define next NEXT using namespace std; const int MAXN = 100000 + 3; const int MOD = (int)1e9 + 7; int is[MAXN], pre[MAXN], next[MAXN]; LL f[MAXN],jie[MAXN]; void init(int n){ jie[0] = 1; for(int i=1;i<=n;i++) jie[i] = jie[i-1] * i % MOD; int now = -1; for(int i=1;i<=n;i++){ pre[i] = now; if(is[i]) now = i; } now = -1; for(int i=n;i>0;i--){ next[i] = now; if(is[i]) now = i; } } LL qp(LL x,LL y){ LL res = 1; while(y){ if(y & 1) res = res * x % MOD; x = x * x % MOD; y >>= 1; } return res; } LL get_c(LL x,LL y){ if(y < 0 || x < y) return 0; if(y == 0 || y == x) return 1; return jie[x] * qp(jie[y] * jie[x - y] % MOD,MOD - 2) % MOD; } LL solve(int n,bool flag){ if(!flag) return qp(2,n - 1); init(n); //for(int i=1;i<=n;i++){ // printf("i = %d is = %d ",i,is[i]); //} int L = n + 1, R = 0; for(int i=1;i<=n;i++){ if(!is[i]) continue; if(L <= is[i] && R >= is[i]) return 0; if(pre[i] == -1 && next[i] == -1){ LL ans = 0,now; for(int x=0;x < is[i];x++){ now = get_c(i-1,x) * get_c(n-i,is[i]-x-1) % MOD; if(x > 1) ans = (ans + now * 2 % MOD) % MOD; else ans = (ans + now) % MOD; } return ans; } else if(pre[i] > 0){ f[i] = f[pre[i]]; //printf("i = %d pre = %d next = %d f = %d ",i,pre[i],next[i],f[i]); if(is[i] > is[pre[i]]) R++; else L--; //printf("L = %d R = %d ",L,R); if(next[i] == -1){ return f[i] * get_c(n-i,L-1) % MOD; } else{ if(is[next[i]] > R){ //printf("i = %d f = %d ",i,f[i]); f[i] = f[i] * get_c(next[i]-i-1,is[next[i]]-R-1) % MOD; R = is[next[i]] - 1; L = R + 2 - next[i]; //printf("i = %d f = %d ",i,f[i]); } else{ //printf("i = %d f = %d ",i,f[i]); f[i] = f[i] * get_c(next[i]-i-1,L-is[next[i]]-1) % MOD; L = is[next[i]] + 1; R = L + next[i] - 2; //printf("i = %d f = %d ",i,f[i]); } } //printf("L = %d R = %d ",L,R); } else{ if(is[i] < is[next[i]]){ R = is[next[i]] - 1; L = R + 2 - next[i]; } else{ L = is[next[i]] + 1; R = L + next[i] - 2; } int cnt = abs(is[next[i]] - is[i]); f[i] = 0; if(i == 1){ f[i] = get_c(next[i]-2,R-is[i]); } else{ //printf("is = %d L = %d R = %d ",is[i],L,R); if(i-1 <= is[i]-L) f[i] = qp(2,i-2) * get_c(next[i]-i-1,is[i]-L-i+1) % MOD; //printf("f = %d ",f[i]); if(i-1 <= R-is[i]) (f[i] += qp(2,i-2) * get_c(next[i]-i-1,R-is[i]-i+1)% MOD) %= MOD; //printf("f = %d ",f[i]); } //printf("i = %d pre = %d next = %d f = %d ",i,pre[i],next[i],f[i]); //printf("L = %d R = %d ",L,R); } } return -1; } int main(){ int n,u; bool flag = false; scanf("%d",&n); memset(is,0,sizeof is); for(int i=1;i<=n;i++){ scanf("%d",&u); if(u){ is[u] = i; flag = true; } } printf("%d ",(int)solve(n,flag)); return 0; }