顾z
你没有发现两个字里的blog都不一样嘛 qwq
题目描述-->p1169 棋盘制作
题目大意
给定一个01棋盘,求其中01交错的最大正方形与矩形。
解题思路:
动态规划---悬线法
以下内容部分参考@Clove_unique
悬线法
用途:
解决给定矩阵中满足条件的最大子矩阵
做法:
用一条线(横竖貌似都行)左右移动直到不满足约束条件或者到达边界
定义几个东西:
(left[i][j]):代表从((i,j))能到达的最左位置
(right[i][j]):代表从((i,j))能到达的最右位置
(up[i][j]):代表从((i,j))向上扩展最长长度.
递推公式:
至于为什么递推公式中考虑上一层的情况?
是因为up数组的定义,up数组代表向上扩展最长长度,
所以需要考虑上一层的情况.
解决
求解正方形&&长方形的情况即可。
题目要求01交错,所以"!="即可
-------------------代码-------------------
#include<bits/stdc++.h>
#define IL inline
#define RI register int
#define maxn 2001
using namespace std;
IL void read(int &x){
int f=1;x=0;char s=getchar();
while(s>'9'||s<'0'){if(s=='-')f=-1;s=getchar();}
while(s<='9'&&s>='0'){x=x*10+s-'0';s=getchar();}
x*=f;
}
int res[maxn][maxn],left[maxn][maxn],right[maxn][maxn],up[maxn][maxn];
int n,m,ans1,ans2;
int main()
{
read(n),read(m);
for(RI i=1;i<=n;i++)
for(RI j=1;j<=m;j++)
{
read(res[i][j]);
left[i][j]=right[i][j]=j;
up[i][j]=1;
}
for(RI i=1;i<=n;i++)
for(RI j=2;j<=m;j++)
if(res[i][j]!=res[i][j-1])
left[i][j]=left[i][j-1];//预处理左边界
for(RI i=1;i<=n;i++)
for(RI j=m-1;j>0;j--)
if(res[i][j]!=res[i][j+1])
right[i][j]=right[i][j+1];//预处理右边界
for(RI i=1;i<=n;i++)
for(RI j=1;j<=m;j++)
{
if(i>1&&res[i][j]!=res[i-1][j])
{
left[i][j]=max(left[i][j],left[i-1][j]);
right[i][j]=min(right[i][j],right[i-1][j]);
up[i][j]=up[i-1][j]+1;
}
int a=right[i][j]-left[i][j]+1; //横向长度
int b=min(a,up[i][j]);//竖向长度
//printf("a:%d b:%d
",a,b);
ans1=max(ans1,b*b);//正方形
ans2=max(ans2,a*up[i][j]);//长方形
}
printf("%d
%d",ans1,ans2);
}
悬线法题目:P1169 棋盘制作 p4147 玉蟾宫 p2701 巨大的牛棚 p1387 最大正方形
UPD
2018.09.26
Q :如图这种情况下,我们根据状态转移方程求出的是黑色部分的面积.而实际上我们更大的面积为红色部分,这样的话,悬线法不就错了?
(如果你也有这方面的疑惑,请细读下面的话)
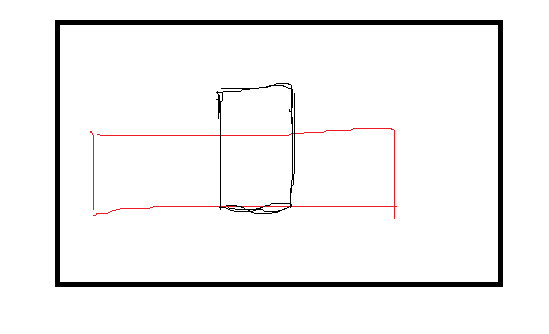
A:红色部分会被考虑到.
考虑我们代码中的这一部分
if(i>1&&res[i][j]!=res[i-1][j])
{
left[i][j]=max(left[i][j],left[i-1][j]);
right[i][j]=min(right[i][j],right[i-1][j]);
up[i][j]=up[i-1][j]+1;
}
if语句执行的条件是(res[i][j]!=res[i-1][j]),即只有满足条件的情况下我们才能更改当前位置((i,j))的(left)数组与(right)数组.
而不满足条件时,我们当前位置((i,j))的(left,right,up)数组并不会改变.
所以说当再次进行状态转移的时候,我们又能根据图中这些未被更新的点(即蓝色部分)的数组去求解出红色部分的面积.

还有一点需要注意的是,在某一行的一段的合法序列中,他们的(left)数组与(right)数组所指位置相同.(这个根据状态转移方程应该不难理解.
例如这样,这一段合法序列中位置的(left[i][j])所指位置皆为红色部分,(right[i][j])所指位置皆为蓝色部分.

如果不能理解的话可以私信问我的 qwq.
已经尽力写的很详细啦