B: Prime Split
题解:
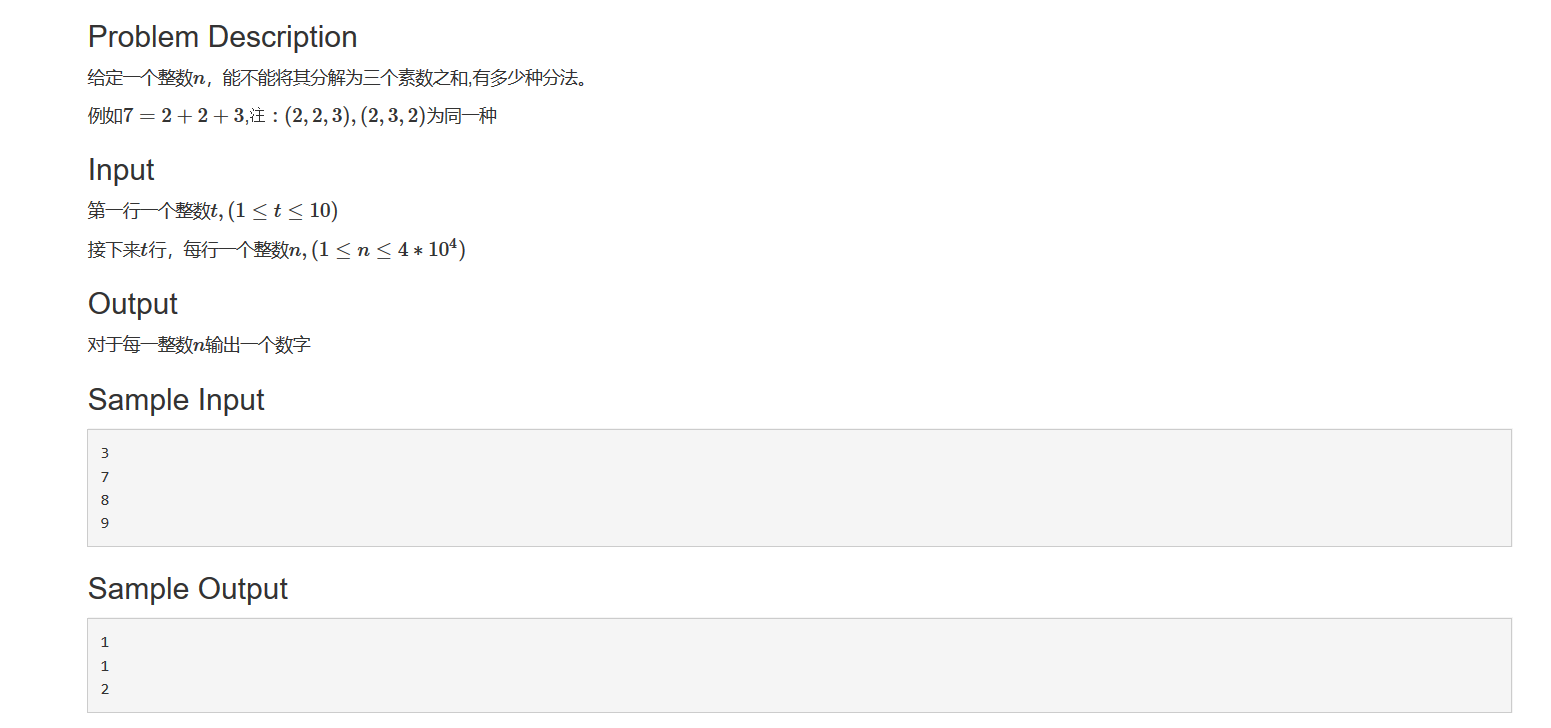
1、先判断两个素数w[i]、w[j]的和是否大于n-2,若小于则说明数字n不可能由三个素数组成(2是最小的素数)
2、再判断n-w[i]-w[j]是否是素数
3、保证w[i]、w[j]、n-w[i]-w[j]是递增的,避免重复计数
//注意laz[]要和线段树数组开一样大小 #include<iostream> #include<algorithm> #include<vector> #include<math.h> #include<stdio.h> #include<string.h> #include<algorithm> using namespace std; const int maxn = 40005; int prim[maxn], w[maxn], cnt = 0;//prim[i]起标记作用,prim[i]==0表示i是质数,注意这里把1也标记成了质数 int x[maxn];//x[i]表示偶数是i的符合条件的两个质数是x[i]和i-x[i]; void init() { memset(prim, false, sizeof(prim)); prim[1]=1;//1不是素数 for(int i = 2; i < maxn; i++) { if(prim[i]) //判断i是否为偶数 continue; w[cnt++] = i;//w存质数 for(int j = i << 1; j < maxn; j+=i)//把所有质数的倍数标记 prim[j] = true; } } int main() { int t,n; cin>>t; init(); while(t--) { cin>>n; int ans=0; for(int i=0;i<cnt;i++) { for(int j=i;j<cnt;j++) { int k=w[i]+w[j]; if(k>n-2)//2是最小的素数,这里判断不可能由三个素数组成的情况 break; int temp=n-k; if(temp<w[j])//保证三个素数w[i],w[j],temp是递增的,避免下面重复计数 continue; if(prim[temp]==0) ans++; } } cout<<ans<<endl; } return 0; }