【SDOI2017】天才黑客（前后缀优化建图 & 最短路）

Description

给定一张有向图，(n) 个点，(m) 条边。第 (i) 条边上有一个边权 (c_i)，以及一个字符串 (s_i)。

其中字符串 (s_1, s_2, cdots , s_m) 组成的字典树的结点数为 (k)。字典树在输入时给出，每个字符串 (s_i) 以一个正整数 (d_i) 的形式给出，表示 (s_i) 对应字典树上的 (d_i) 号结点。

若一条路径经过的边依次为 (e_1, e_2,cdots, e_p)，那么路径的长度定义为 (sum_{i=1}^p c_{e_i} + sum_{i=1}^{p-1}operatorname{lcp}(s_{e_i}, s_{e_{i+1}}))。其中 (operatorname{lcp}(s, t)) 表示字符串 (s, t) 最长公共前缀的长度。

求顶点 (1) 开始的单源最短路径。共 (T(le 10)) 组数据。

Hint

(1le n, mle 5 imes 10^4, 1le k, c_ile 2 imes 10^4)

Solution

下面复杂度中 (n, m,k) 同阶

观察题目，发现路径长的计算涉及到相邻两条边的 ( ext{lcp})，即使直接暴力跑 Dijkstra 也非常不方便，不如将这个图乱搞一波，最好跑最短路时可以直接上板子。那么考虑怎样优秀地建图。

考虑把边变成虚点，然后试着把 ( ext{lcp}) 部分以 虚点间再连虚边 的方式，达到转化掉这个“相邻”的目的。具体地，假如说存在两条边 (u o v, v o w)，边权分别为 (c_i, c_j)，字符串分别为 (s_i, s_j)，那么我们建立虚点 (t(i), t(j))，点权分别为 (c_i, c_j)，并有一条 (t(i) o t(j)) 的边且边权为 ( ext{lcp}(s_i, s_j))。( ext{lcp}) 即为给定 Trie 树上的 LCA 的深度。

但这样还是不太舒服，我们再把点权化掉：我们对一条边建 两个虚点 而不是一个，分别作为入点和出点。对于第 (i) 条边的入点和出点分别记做 (t_{in}(i), t_{out}(i))。那么原先的点权我们可以放到 (t_{in}(i) o t_{out}(i)) 这条边上。

如果把图建出来了，那么是可以套 Dijkstra 板子的。不过如果有一个菊花图，那么会存在 (O(m^2)) 条虚边，时空两爆炸。

---

考虑这样一个问题，对于 Trie 上的结点 (r_1, r_2, cdots, r_R)，我们要求所有结点间的 LCA 的深度。如果我们将 (r) 先按 Trie 的 DFS 序 排序，那么可以发现：( ext{depth}( ext{LCA}(r_i, r_j)) = min_{ile k<j}{ ext{depth}( ext{LCA}(r_k, r_{k+1}))})。也就是说，我们只要求出相邻两个的 LCA，其他都可以用 区间最小值 表示。

把这个思路套到这道题上，我们将一个点 (x) 的所有出边的入点，所有入边的出点（就是 (x) 周围一圈），分别按 Trie 的 DFS 序排序，然后我们发现这是一个 点向区间，区间向点 连边的问题，于是维护两颗线段树来优化连边即可，这样总边数只有 (O(nlog n)) 条。

现在我们得到了一个 (O(nlog^2 n)) 时间的算法，写的好理论上就能过了。

---

其实还可以优化，我们其实不需要线段树。

如果出点、入点排序后的结果为 ({a_1, a_2, cdots, a_A}, {b_1, b_2, cdots, b_B})，假如 (a_i o b_j) 的虚边对应 ( ext{lcp}) 大小为 (l)，那么 出点 (a_1, a_2, cdots , a_i) 都能以不超过 (l) 的代价到达出点 (b_j, b_{j+1}, cdots ,b_B)。那么本质上是一段 前缀 向一段 后缀 连边。

于是我们就可以：

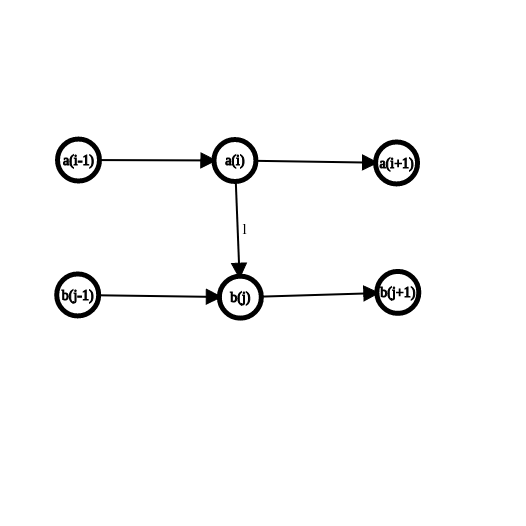
连接 (a_i, a_{i+1}) 和 (b_i, b_{i+1}) 的边权我们设为 (0)。这样就只需要计算 DFS 序相邻的就行了，总边数被控制在了 (O(m))。

但是这样只能处理 (ile j) 时 (a_i o b_j) 的情况，如果 (i>j) 是不是无法处理呢？

显然可以，我们只要一开始将一条边拆成 (4) 个虚点，两个入点，两个出点，每个入点都想两个出点连边。然后对于其中一对出入点我们如上述建边，然后另外一对我们只要把上图的 (0) 边 反着建 即可。

这就是所谓的 前后缀优化建图。

加上 Dijkstra 的复杂度这题的时间为 (O(nlog n))。

Code

建图是本题的精髓，建议自己在纸上画一画。

/*
 * Author : _Wallace_
 * Source : https://www.cnblogs.com/-Wallace-/
 * Problem : SDOI2017 天才黑客
 */
#include <algorithm>
#include <cstring>
#include <iostream>
#include <vector>
#include <queue>

using namespace std;
const int N = 5e4 + 5;
const int K = 2e4 + 5;
const int LogK = 17;

int n, m, k;
struct Edge {
    int to, len;
    Edge(int a, int b) : to(a), len(b) { }
};
vector<Edge> adj[N << 2];
vector<int> trie[K];

int c;
void link(int u, int v, int w) { adj[u].emplace_back(v, w); ++c;}
template<int x> int get(int e) { return (e - 1) * 4 + x; }
/*1/3 out 2/4 in*/

int fa[K][LogK], dep[K], dfn[K], timer = 0;
void initLCA(int x, int f) {
    dep[x] = dep[fa[x][0] = f] + 1, dfn[x] = ++timer;
    for (int j = 1; j < LogK; j++) fa[x][j] = fa[fa[x][j - 1]][j - 1];
    for (auto y : trie[x]) if (y != f) initLCA(y, x);
}
int lca(int x, int y) {
    if (dep[x] < dep[y]) swap(x, y);
    for (int j = LogK - 1; ~j; --j) if (dep[fa[x][j]] >= dep[y]) x = fa[x][j];
    if (x == y) return x;
    for (int j = LogK - 1; ~j; --j) if (fa[x][j] != fa[y][j]) x = fa[x][j], y = fa[y][j];
    return fa[x][0];
}

vector<int> in[N];
vector<int> out[N];
int pos[N];

bool cmp1(int x, int y) { return dfn[pos[x]] < dfn[pos[y]]; }
bool cmp2(pair<int, bool> a, pair<int, bool> b) { return cmp1(a.first, b.first); }
void build(int x) {
    if (in[x].empty() || out[x].empty()) return;
    sort(in[x].begin(), in[x].end(), cmp1), sort(out[x].begin(), out[x].end(), cmp1);

    for (int i = 1; i < in[x].size(); i++) link(get<2>(in[x][i - 1]), get<2>(in[x][i]), 0);
    for (int i = 1; i < in[x].size(); i++) link(get<4>(in[x][i]), get<4>(in[x][i - 1]), 0);
    for (int i = 1; i < out[x].size(); i++) link(get<1>(out[x][i - 1]), get<1>(out[x][i]), 0);
    for (int i = 1; i < out[x].size(); i++) link(get<3>(out[x][i]), get<3>(out[x][i - 1]), 0);

    vector<pair<int, bool> > rec;
    for (auto v : in[x]) rec.emplace_back(v, 0);
    for (auto v : out[x]) rec.emplace_back(v, 1);
    sort(rec.begin(), rec.end(), cmp2);

    for (int t = 0, i = 0, j = 0; t < rec.size() - 1; t++) {
        rec[t].second ? ++j : ++i;
        int val = dep[lca(pos[rec[t].first], pos[rec[t + 1].first])] - 1;
        if (i > 0 && j < out[x].size()) link(get<2>(in[x][i - 1]), get<1>(out[x][j]), val);
        if (j > 0 && i < in[x].size()) link(get<4>(in[x][i]), get<3>(out[x][j - 1]), val);
    }
}

priority_queue< pair<long long, int>,
                vector<pair<long long, int> >,
                greater<pair<long long, int> > > Q;
long long dist[N << 2];
bool book[N << 2];
void dijkstra() {
    memset(dist, 0x3f, sizeof(dist));
    memset(book, false, sizeof(book));
    for (auto x : out[1]) Q.emplace(dist[get<1>(x)] = 0ll, get<1>(x));
    for (auto x : out[1]) Q.emplace(dist[get<3>(x)] = 0ll, get<3>(x));
    for (int x; !Q.empty(); ) {
        x = Q.top().second, Q.pop();
        if (book[x]) continue; book[x] = 1;
        for (auto y : adj[x]) if (dist[y.to] > dist[x] + y.len)
            Q.emplace(dist[y.to] = dist[x] + y.len, y.to);
    }
    for (int i = 2; i <= n; i++) {
        long long ans = 1e18;
        for (auto x : in[i]) ans = min(ans, dist[get<2>(x)]);
        for (auto x : in[i]) ans = min(ans, dist[get<4>(x)]);
        cout << ans << endl;
    }
}

void solve(){
    cin >> n >> m >> k;
    for (int i = 1; i <= n; i++) in[i].clear(), out[i].clear();
    for (int i = 1; i <= k; i++) trie[i].clear();
    for (int i = 1; i <= m * 4; i++) adj[i].clear();

    for (int i = 1, u, v, w; i <= m; i++) {
        cin >> u >> v >> w >> pos[i];
        in[v].emplace_back(i), out[u].emplace_back(i);
        link(get<1>(i), get<2>(i), w), link(get<1>(i), get<4>(i), w);
        link(get<3>(i), get<2>(i), w), link(get<3>(i), get<4>(i), w);
    }
    for (int i = 1, u, v, w; i < k; i++) {
        cin >> u >> v >> w;
        trie[u].emplace_back(v);
        trie[v].emplace_back(u);
    }

    initLCA(1, 0);
    for (int i = 2; i <= n; i++) build(i);
    dijkstra();
}
signed main() {
    ios::sync_with_stdio(false);
    int T; for (cin >> T; T; --T) solve();
}